Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Question 3

1pts
Find the length of an arc whose central angle measures
90^(@) that is on a circle whose diameter is 20 .

2pi

4pi

5pi

10 pi

Question $3$ $\newline$ $1$ pts $\newline$ Find the length of an arc whose central angle measures $\newline$ $90^\circ$ that is on a circle whose diameter is $20$ . $\newline$ $2\pi$ $\newline$ $4\pi$ $\newline$ $5\pi$ $\newline$ $10\pi$

View step-by-step help

View step-by-step help

Find Coordinate on Unit Circle

Full solution

Q. Question

3

\newline

1

pts

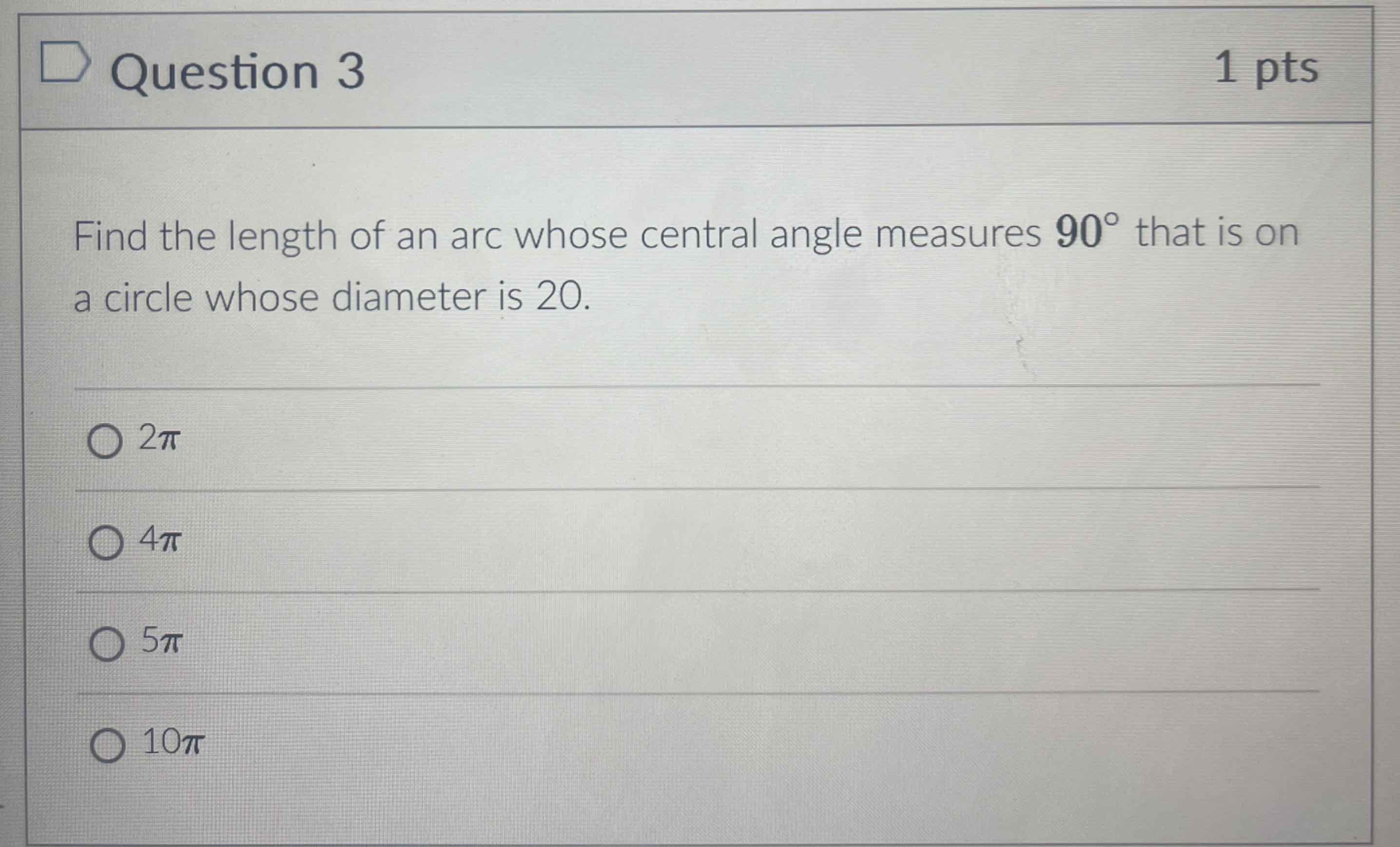
\newline

Find the length of an arc whose central angle measures

\newline

90^\circ

that is on a circle whose diameter is

20

.

\newline

2\pi

\newline

4\pi

\newline

5\pi

\newline

10\pi

Identify arc length formula: Step $1$ : Identify the formula for the length of an arc. $\newline$ The formula for the length of an arc $s$ is $s = r\theta$ , where $r$ is the radius of the circle and $\theta$ is the central angle in radians.
Convert angle to radians: Step $2$ : Convert the central angle from degrees to radians. $\newline$ Given angle = $90$ degrees. To convert degrees to radians, multiply by $\pi/180$ . $\newline$ $\theta = 90 \times (\pi/180) = \pi/2$ radians.
Calculate circle radius: Step $3$ : Calculate the radius of the circle. $\newline$ The diameter of the circle is given as $20$ . The radius $(r)$ is half of the diameter. $\newline$ $r = \frac{20}{2} = 10$ .
Calculate arc length: Step $4$ : Calculate the length of the arc using the formula. $\newline$ Substitute $r = 10$ and $\theta = \frac{\pi}{2}$ into the formula $s = r\theta$ . $\newline$ $s = 10 \times \left(\frac{\pi}{2}\right) = 5\pi$ .

More problems from Find Coordinate on Unit Circle

Question

Marco's class is painting a mural on the side of their school. The mural covers a

3 \frac{1}{2} \mathrm{~m}

high, rectangular wall. It has an area of

28 \mathrm{~m}^{2}

\newline

What is the length of the mural?

\newline

Posted 3 months ago

Question

A cup of hot coffee has been left to cool in a room with an ambient temperature of

21^{\circ} \mathrm{C}

\newline

The relationship between the elapsed time,

m

, in minutes, since the coffee was left to cool, and the temperature of the coffee,

T

{ }^{\circ} \mathrm{C}

, is modeled by the following function.

\newline

T(m)=21+74 \cdot 10^{-0.03 m}

\newline

What will the temperature of the coffee be after

10

\newline

Round your answer, if necessary, to the nearest hundredth.

\newline

{ }^{\circ} C

Posted 3 months ago

Question

Takumi plants a tree in his backyard and studies how the number of branches grows over time.

\newline

He predicts that the relationship between

N

, the number of branches on the tree, and

t

, the elapsed time, in years, since the tree was planted can be modeled by the following equation.

\newline

N=5 \cdot 10^{0.3 t}

\newline

According to Takumi's model, in how many years will the tree have

100

\newline

Give an exact answer expressed as a base

-10

\newline

Posted 3 months ago

Question

g(x)=2^{x}

\newline

Can we use the mean value theorem to say the equation

g^{\prime}(x)=16

has a solution where

3<x<5

\newline

1

\newline

(A) No, since the function is not differentiable on that interval.

\newline

(B) No, since the average rate of change of

g

over the interval

3 \leq x \leq 5

1 \overline{6}

\newline

(C) Yes, both conditions for using the mean value theorem have been met.

Posted 3 months ago

Question

\frac{d}{d x}\left(\frac{x^{2}-x+5}{4 x-1}\right)=

Posted 3 months ago

Question

\frac{d}{d x}\left(\frac{2 x^{2}+x-3}{2 x+7}\right)=

Posted 3 months ago

Question

\frac{d}{d x}\left(\frac{3 x^{2}-1}{x-2}\right)=

Posted 3 months ago

Question

\frac{d y}{d t}=2 t+3 \text { and } y(1)=6

\newline

t

y=0

\newline

Choose all answers that apply:

\newline

t=-1

\newline

t=-3

\newline

t=0

\newline

t=-4

\newline

t=1

\newline

t=-2

Posted 3 months ago

Question

\frac{d}{d x}\left(x^{\frac{3}{4}}\right)=

Posted 3 months ago

Question

y=x^{13}

\newline

\frac{d y}{d x}=

Posted 3 months ago