Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

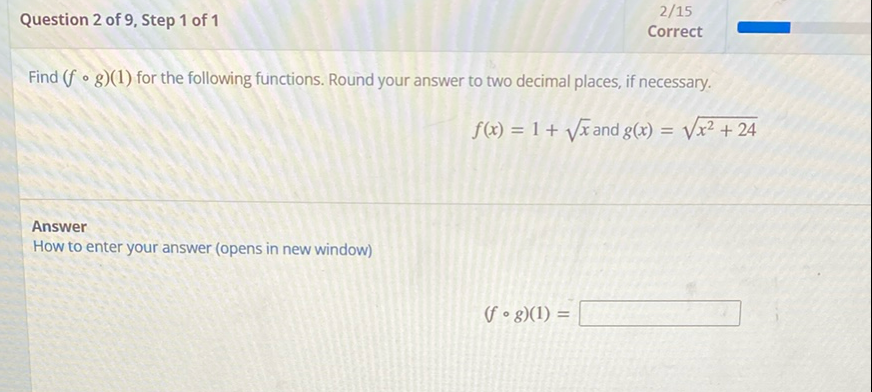
Question 2 of 9 , Step 1 of 1 2//15 Correct Find (f@g)(1) for the following functions. Round your answer to two decimal places, if necessary. f(x)=1+sqrtx" and "g(x)=sqrt(x^(2)+24) Answer How to enter your answer (opens in new window) (f@g)(1)=

\newlineFind (f∘g)(1) (f \circ g)(1) for the following functions. Round your answer to two decimal places, if necessary.\newlinef(x)=1+x and g(x)=x2+24 f(x)=1+\sqrt{x} \text { and } g(x)=\sqrt{x^{2}+24} \newlineAnswer\newlineHow to enter your answer (opens in new window)\newline(f∘g)(1)= (f \circ g)(1)=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 8right chevron icon
Evaluate variable expressions for sequencesright chevron icon

Full solution

Q. \newlineFind (f∘g)(1) (f \circ g)(1) for the following functions. Round your answer to two decimal places, if necessary.\newlinef(x)=1+x and g(x)=x2+24 f(x)=1+\sqrt{x} \text { and } g(x)=\sqrt{x^{2}+24} \newlineAnswer\newlineHow to enter your answer (opens in new window)\newline(f∘g)(1)= (f \circ g)(1)=
  1. Find g(1)g(1): To find (f∘g)(1)(f\circ g)(1), we first need to evaluate g(1)g(1) and then plug that result into the function ff.
  2. Evaluate g(1)g(1): Evaluate g(1)g(1) by substituting xx with 11 in the function g(x)=x2+24g(x) = \sqrt{x^2 + 24}.
    g(1)=12+24g(1) = \sqrt{1^2 + 24}
    g(1)=1+24g(1) = \sqrt{1 + 24}
    g(1)=25g(1) = \sqrt{25}
    g(1)=5g(1) = 5
  3. Substitute into ff: Now that we have g(1)=5g(1) = 5, we substitute this value into the function ff to find (f@g)(1)(f@g)(1).\newline(f@g)(1)=f(g(1))=f(5)(f@g)(1) = f(g(1)) = f(5)
  4. Evaluate f(5)f(5): Evaluate f(5)f(5) by substituting xx with 55 in the function f(x)=1+xf(x) = 1 + \sqrt{x}.\newlinef(5)=1+5f(5) = 1 + \sqrt{5}\newlinef(5)=1+2.236f(5) = 1 + 2.236 (rounded to three decimal places for intermediate calculation)\newlinef(5)=3.236f(5) = 3.236 (rounded to three decimal places for intermediate calculation)
  5. Round final answer: Round the final answer to two decimal places as instructed.\newline(f@g)(1)=3.24(f@g)(1) = 3.24 (rounded to two decimal places)

More problems from Evaluate variable expressions for sequences

Question
Find the sum of the finite arithmetic series. ∑n=110(7n+4)\sum_{n=1}^{10} (7n+4)\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`
Get tutor helpright-arrow

Posted 1 month ago

Question
Type the missing number in this sequence: `2, 4 8`, ______,`32`
Get tutor helpright-arrow

Posted 2 months ago

Question
What kind of sequence is this? 2,10,50,250,…2, 10, 50, 250, \ldots Choices:Choices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the missing number in this pattern? 1,4,9,16,25,36,49,64,81,____1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_
Get tutor helpright-arrow

Posted 1 month ago

Question
Classify the series. ∑n=012(n+2)3 \sum_{n = 0}^{12} (n + 2)^3 \newlineChoices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the first three partial sums of the series.\newline1+6+11+16+21+26+⋯1 + 6 + 11 + 16 + 21 + 26 + \cdots\newlineWrite your answers as integers or fractions in simplest form.\newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the third partial sum of the series. \newline3+9+15+21+27+33+⋯3 + 9 + 15 + 21 + 27 + 33 + \cdots\newlineWrite your answer as an integer or a fraction in simplest form. \newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the first three partial sums of the series. \newline1+7+13+19+25+31+⋯1 + 7 + 13 + 19 + 25 + 31 + \cdots\newlineWrite your answers as integers or fractions in simplest form. \newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Does the infinite geometric series converge or diverge?\newline1+34+916+2764+⋯1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots\newlineChoices:\newline[A]converge\text{[A]converge}\newline[B]diverge\text{[B]diverge}
Get tutor helpright-arrow

Posted 1 month ago

View all (21)