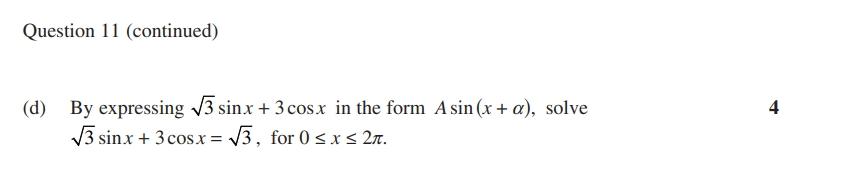By expressing $\newline$ $\sqrt{3}\sin x+3\cos x$ in the form $A \sin(x+\alpha)$ , solve $\sqrt{3}\sin x+3\cos x=\sqrt{3}$ , for $\newline$ $0 \leq x \leq 2\pi$ .

View step-by-step help

Home

Math Problems

Algebra 2

Simplify radical expressions with variables II

Full solution

Q. By expressing

\newline

\sqrt{3}\sin x+3\cos x

in the form

A \sin(x+\alpha)

, solve

\sqrt{3}\sin x+3\cos x=\sqrt{3}

, for

\newline

0 \leq x \leq 2\pi

Use Trigonometric Identity: We want to express $\sqrt{3}\sin(x) + 3\cos(x)$ in the form $A \sin(x+\alpha)$ . To do this, we will use the identity $\sin(x+\alpha) = \sin(x)\cos(\alpha) + \cos(x)\sin(\alpha)$ .
Match Coefficients: Let $A \sin(x+\alpha) = A(\sin(x)\cos(\alpha) + \cos(x)\sin(\alpha))$ . We want to match the coefficients of $\sin(x)$ and $\cos(x)$ to those in $\sqrt{3}\sin(x) + 3\cos(x)$ .
Solve Equations for $A$ : Matching coefficients, we get $A \cos(\alpha) = \sqrt{3}$ and $A \sin(\alpha) = 3$ . We can solve these two equations to find $A$ and $\alpha$ .
Find A Using Pythagorean Identity: To find A, we use the Pythagorean identity: $A^2 = (A \cos(\alpha))^2 + (A \sin(\alpha))^2$ . Substituting the values we have $A^2 = (\sqrt{3})^2 + 3^2 = 3 + 9 = 12$ .
Find $A$ and $\Alpha$ : Taking the square root of both sides, we get $A = \sqrt{12} = 2\sqrt{3}$ .
Express in Desired Form: To find $\alpha$ , we take the ratio of the two equations: $\tan(\alpha) = \frac{A \sin(\alpha)}{A \cos(\alpha)} = \frac{3}{\sqrt{3}} = \sqrt{3}$ .
Isolate $\sin(x + \alpha)$ : Using the $\arctan$ function, we find $\alpha = \arctan(\sqrt{3})$ . Since we are looking for solutions in the interval $[0, 2\pi]$ , we consider the principal value of $\arctan(\sqrt{3})$ , which is $\pi/3$ .
Find Solutions for $\sin(y)$ : Now we have expressed $\sqrt{3}\sin(x) + 3\cos(x)$ as $2 \sqrt{3} \sin(x + \pi/3)$ . We can now solve the equation $2 \sqrt{3} \sin(x + \pi/3) = \sqrt{3}$ .
Substitute $x + \alpha$ for $y$ : Divide both sides by $2 \sqrt{3}$ to isolate $\sin(x + \pi/3)$ : $\sin(x + \pi/3) = \frac{\sqrt{3}}{2 \sqrt{3}} = \frac{1}{2}$ .
Solve for x: We look for solutions to $\sin(x + \frac{\pi}{3}) = \frac{1}{2}$ . The solutions to $\sin(y) = \frac{1}{2}$ are $y = \frac{\pi}{6} + 2k\pi$ and $y = \frac{5\pi}{6} + 2k\pi$ , where $k$ is an integer.
Check Solutions in Interval: Substitute $x + \frac{\pi}{3}$ for $y$ : $x + \frac{\pi}{3} = \frac{\pi}{6} + 2k\pi$ or $x + \frac{\pi}{3} = \frac{5\pi}{6} + 2k\pi$ . We solve for $x$ in each case.
Final Solutions: For the first equation: $x = \frac{\pi}{6} - \frac{\pi}{3} + 2k\pi = -\frac{\pi}{6} + 2k\pi$ . For the second equation: $x = \frac{5\pi}{6} - \frac{\pi}{3} + 2k\pi = \frac{\pi}{2} + 2k\pi$ .
Final Solutions: For the first equation: $x = \frac{\pi}{6} - \frac{\pi}{3} + 2k\pi = -\frac{\pi}{6} + 2k\pi$ . For the second equation: $x = \frac{5\pi}{6} - \frac{\pi}{3} + 2k\pi = \frac{\pi}{2} + 2k\pi$ .We need to find the values of $x$ in the interval $[0, 2\pi]$ . For the first equation, $x = -\frac{\pi}{6}$ is not in the interval, but $x = -\frac{\pi}{6} + 2\pi = \frac{11\pi}{6}$ is. For the second equation, $x = \frac{\pi}{2}$ is in the interval.
Final Solutions: For the first equation: $x = \frac{\pi}{6} - \frac{\pi}{3} + 2k\pi = -\frac{\pi}{6} + 2k\pi$ . For the second equation: $x = \frac{5\pi}{6} - \frac{\pi}{3} + 2k\pi = \frac{\pi}{2} + 2k\pi$ .We need to find the values of $x$ in the interval $[0, 2\pi]$ . For the first equation, $x = -\frac{\pi}{6}$ is not in the interval, but $x = -\frac{\pi}{6} + 2\pi = \frac{11\pi}{6}$ is. For the second equation, $x = \frac{\pi}{2}$ is in the interval.The solutions to the equation $\sqrt{3}\sin(x) + 3\cos(x) = \sqrt{3}$ in the interval $[0, 2\pi]$ are $x = \frac{11\pi}{6}$ and $x = \frac{\pi}{2}$ .