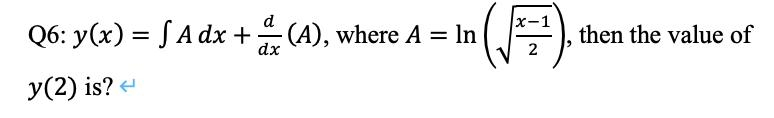Q6: y(x)=int Adx+(d)/(dx)(A), where A=ln(sqrt((x-1)/(2))), then the value of y(2) is?

Question

Q6:  y(x)=int Adx+(d)/(dx)(A), where  A=ln(sqrt((x-1)/(2))), then the value of  y(2) is?

Bytelearn · Accepted Answer

Find Expression for A: First, we need to find the expression for A, which is given as A = ln(sqrt((x-1)/2)). We can simplify this expression by using the property of logarithms that ln(sqrt(x)) = (1/2)ln(x). Calculation: A = (1/2)ln((x-1)/2)Find Derivative of A: Next, we need to find the derivative of A with respect to x, which is denoted as (d/dx)(A). To do this, we use the chain rule and the derivative of ln(x) which is 1/x. Calculation: (d/dx)(A) = (1/2)(1/((x-1)/2))(d/dx)((x-1)/2) = (1/2)(2/(x-1))(1/2) = 1/(x-1)Find Integral of A: Now, we need to find the integral of A with respect to x. The integral of ln(x) is xln(x) - x, so we apply this to our function A. Calculation: ∫A dx = ∫(1/2)ln((x-1)/2) dx = (1/2)(xln((x-1)/2) - (x-1))Combine Integral and Derivative: We now have the expressions for both the integral of A and the derivative of A. The function y(x) is the sum of these two expressions. So, we add them together. Calculation: y(x) = (1/2)(xln((x-1)/2) - (x-1)) + 1/(x-1)Evaluate y(2): Finally, we need to evaluate y(x) at x = 2. We substitute x with 2 in the expression we found for y(x). Calculation: y(2) = (1/2)(2ln((2-1)/2) - (2-1)) + 1/(2-1) = (1/2)(2ln(1/2) - 1) + 1Simplify Final Expression: We can further simplify the expression by calculating the natural logarithm of 1/2 and the arithmetic operations. Calculation: y(2) = (1/2)(2(-ln(2)) - 1) + 1 = (-ln(2) - 1/2) + 1 = -ln(2) + 1/2

Q $6$ : $y(x)=\int A d x+\frac{d}{d x}(A)$ , where $A=\ln \left(\sqrt{\frac{x-1}{2}}\right)$ , then the value of $y(2)$ is?

Full solution

More problems from Evaluate radical expressions

Related topics

Q666: y(x)=∫Adx+ddx(A) y(x)=\int A d x+\frac{d}{d x}(A) y(x)=∫Adx+dxd​(A), where A=ln⁡(x−12) A=\ln \left(\sqrt{\frac{x-1}{2}}\right) A=ln(2x−1​​), then the value of y(2) y(2) y(2) is?

Q $6$ : $y(x)=\int A d x+\frac{d}{d x}(A)$ , where $A=\ln \left(\sqrt{\frac{x-1}{2}}\right)$ , then the value of $y(2)$ is?