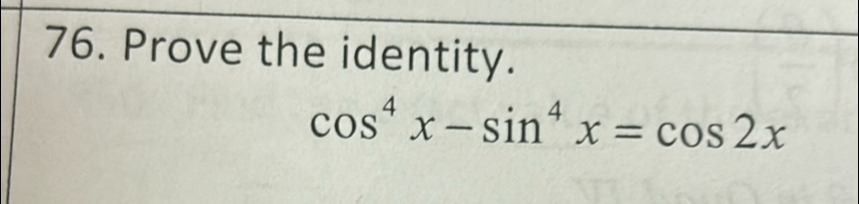AI tutor
Full solution
Q. . Prove the identity.
- Apply Pythagorean identity: We will start by using the Pythagorean identity to rewrite the left side of the equation in terms of cosines only.We can express as to get:
- Rewrite in terms of cosines: Now we will expand the squared terms:
- Expand and simplify: Next, we simplify the expression by combining like terms:
- Use double angle formula: We recognize that is the double angle formula for cosine:
- Final result: We have shown that the left side of the equation simplifies to the right side:
More problems from Solve complex trigonomentric equations
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help