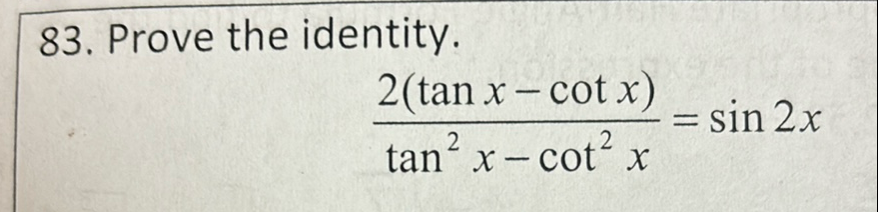Prove the identity. (2(tan x-cot x))/(tan^(2)x-cot^(2)x)=sin 2x

Question

Prove the identity.   (2(tan x-cot x))/(tan^(2)x-cot^(2)x)=sin 2x

Bytelearn · Accepted Answer

Start Problem: Start with the left-hand side of the identity. We have the expression (2(tan x - cot x)) / (tan^2(x) - cot^2(x)).Recall Identities: Recall the Pythagorean identity for tangent and cotangent. tan^2(x) + 1 = sec^2(x) and cot^2(x) + 1 = csc^2(x). We can rewrite the denominator of the left-hand side using these identities. tan^2(x) - cot^2(x) = (sec^2(x) - 1) - (csc^2(x) - 1).Rewrite Denominator: Simplify the denominator. (sec^2(x) - 1) - (csc^2(x) - 1) = sec^2(x) - csc^2(x).Simplify Denominator: Use the reciprocal identities for sec(x) and csc(x). sec(x) = 1/cos(x) and csc(x) = 1/sin(x). So, sec^2(x) - csc^2(x) = (1/cos^2(x)) - (1/sin^2(x)).Use Reciprocal Identities: Find a common denominator for the terms in the denominator. (1/cos^2(x)) - (1/sin^2(x)) = (sin^2(x) - cos^2(x)) / (sin^2(x)cos^2(x)).Find Common Denominator: Recall the double-angle identity for sine. sin(2x) = 2sin(x)cos(x). We can rewrite the numerator of the left-hand side using the tangent and cotangent definitions. tan x = sin(x)/cos(x) and cot x = cos(x)/sin(x). So, 2(tan x - cot x) = 2((sin(x)/cos(x)) - (cos(x)/sin(x))).Rewrite Numerator: Find a common denominator for the terms in the numerator. 2((sin(x)/cos(x)) - (cos(x)/sin(x))) = 2(sin^2(x) - cos^2(x)) / (sin(x)cos(x)).Combine Numerator and Denominator: Combine the numerator and denominator. (2(sin^2(x) - cos^2(x)) / (sin(x)cos(x))) / ((sin^2(x) - cos^2(x)) / (sin^2(x)cos^2(x))).Simplify Complex Fraction: Simplify the complex fraction. The (sin^2(x) - cos^2(x)) terms cancel out, leaving us with: (2 / (sin(x)cos(x))) / (1 / (sin^2(x)cos^2(x))) = 2sin(x)cos(x).Recognize Double-Angle Identity: Recognize that 2sin(x)cos(x) is the double-angle identity for sine. 2sin(x)cos(x) = sin(2x).Conclude Proof: Conclude that the left-hand side is equal to the right-hand side. Therefore, (2(tan x - cot x)) / (tan^2(x) - cot^2(x)) = sin(2x), proving the identity.

$83$ . Prove the identity. $\newline$ $\frac{2(\tan x-\cot x)}{\tan ^{2} x-\cot ^{2} x}=\sin 2 x$

Full solution

More problems from Multiplication with rational exponents

Related topics

838383. Prove the identity.\newline2(tan⁡x−cot⁡x)tan⁡2x−cot⁡2x=sin⁡2x \frac{2(\tan x-\cot x)}{\tan ^{2} x-\cot ^{2} x}=\sin 2 x tan2x−cot2x2(tanx−cotx)​=sin2x

$83$ . Prove the identity. $\newline$ $\frac{2(\tan x-\cot x)}{\tan ^{2} x-\cot ^{2} x}=\sin 2 x$