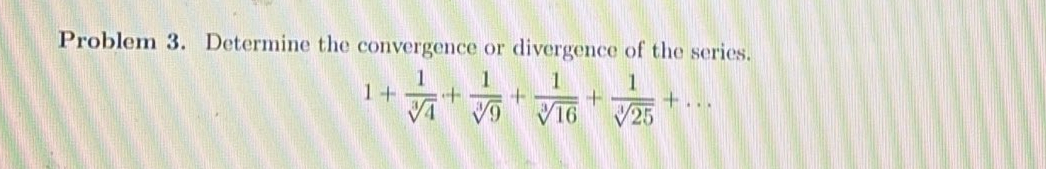Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Determine the convergence or divergence of the series.

1+(1)/(root(3)(4))+(1)/(root(3)(9))+(1)/(root(3)(16))+(1)/(root(3)(25))+dots

Determine the convergence or divergence of the series. $\newline$ $1+\frac{1}{\sqrt[3]{4}}+\frac{1}{\sqrt[3]{9}}+\frac{1}{\sqrt[3]{16}}+\frac{1}{\sqrt[3]{25}}+\dots$

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q. Determine the convergence or divergence of the series.

\newline

1+\frac{1}{\sqrt[3]{4}}+\frac{1}{\sqrt[3]{9}}+\frac{1}{\sqrt[3]{16}}+\frac{1}{\sqrt[3]{25}}+\dots

Identify series type: Step $1$ : Identify the series type. $\newline$ We're dealing with the series $1 + 1/\sqrt[3]{4} + 1/\sqrt[3]{9} + 1/\sqrt[3]{16} + 1/\sqrt[3]{25} + \ldots$ $\newline$ This looks like a p-series where each term is of the form $1/\sqrt[3]{n^2}$ .
Compare with convergent series: Step $2$ : Compare to a known convergent series. $\newline$ For p-series, $\sum \frac{1}{n^p}$ converges if $p > 1$ . Here, $p = \frac{2}{3}$ (since the cube root of $n^2$ is $n^{\frac{2}{3}}$ ).

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 3 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 3 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 2 months ago

Question

\newline

32^{(-1/5)}

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 2 months ago