Full solution
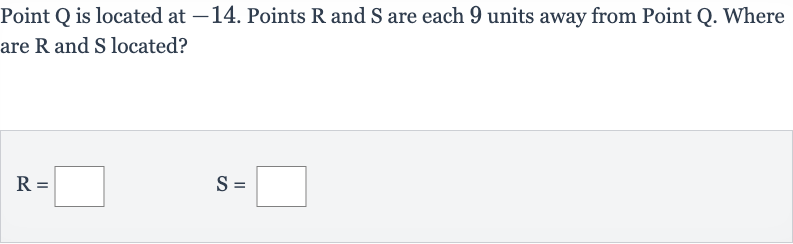
Q. Point is located at . Points and are each units away from Point . Where are and located?
- Understand the problem: Understand the problem.We are given a point on a number line at . We need to find two points, and , that are each units away from . This means we will find two points, one to the left and one to the right of , since a number line extends in both directions.
- Find point R: Find the location of point R.To find point R, which is units away from Q to the left on the number line, we subtract from the position of Q.So, .
- Find point S: Find the location of point S.To find point S, which is units away from Q to the right on the number line, we add to the position of Q.So, .
More problems from Solve trigonometric equations
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help