AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
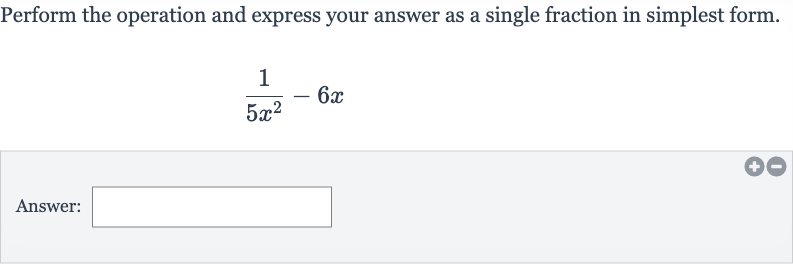
Perform the operation and express your answer as a single fraction in simplest form.Answer:
Full solution
Q. Perform the operation and express your answer as a single fraction in simplest form.Answer:
- Identify Given Expression: Identify the given expression and the operation to be performed.We are given the expression and we need to simplify it.
- Recognize Type of Problem: Recognize that the expression is not a fraction subtraction problem but rather a polynomial with a fraction and a whole term.We need to find a common denominator to combine the terms into a single fraction.
- Determine Least Common Denominator: Determine the least common denominator (LCD) for the terms.The LCD for and (considering the term as ) is .
- Rewrite Terms with LCD: Rewrite each term with the common denominator.The first term is already over the common denominator, so it remains . The second term, , needs to be written with the common denominator, which gives us .
- Perform Multiplication: Perform the multiplication in the second term.Multiplying by gives us . So now we have .
- Combine Terms Over LCD: Combine the terms over the common denominator.Now we can combine the terms to get a single fraction: .
- Simplify Numerator: Simplify the numerator by adding the opposite.The numerator simplifies to , so the fraction becomes .
- Check Further Simplification: Check if the fraction can be simplified further.The fraction cannot be simplified further because the numerator and denominator do not have common factors other than .
