Full solution
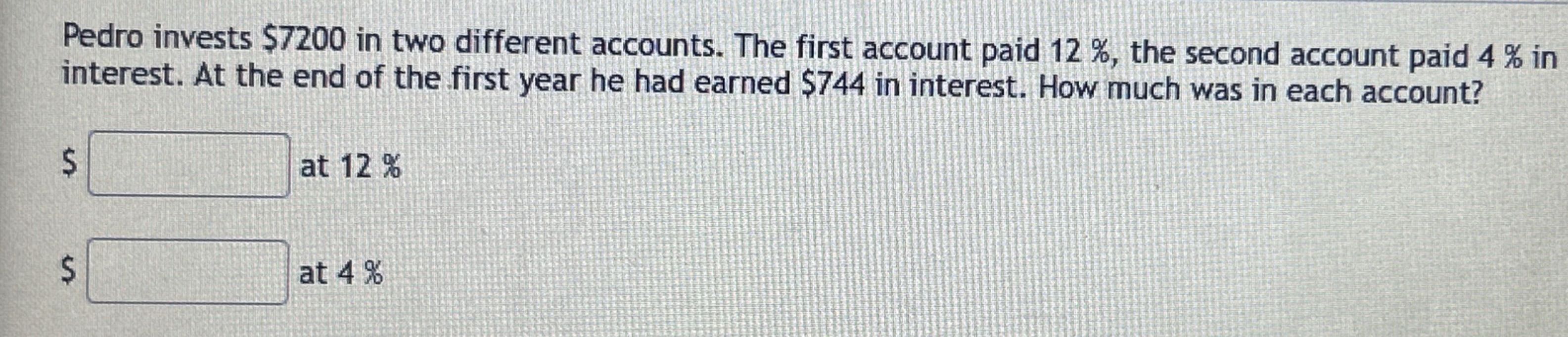
Q. Pedro invests in two different accounts. The first account paid , the second account paid in interest. At the end of the first year he had earned in interest. How much was in each account? ◻ at ◻ at
- Define Variables: Let's denote the amount invested in the \% account as and the amount in the \% account as . We know the total investment is , so:
- Calculate Total Interest: Next, we calculate the total interest from both accounts. The interest from the first account is of , and from the second account, it's of . The total interest earned is , so:
- Solve for y: Now, we solve these equations simultaneously. First, solve the first equation for :
- Substitute in Equation: Substitute in the interest equation:
- Find : Divide by to find :
More problems from Multi-step problems with percents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help