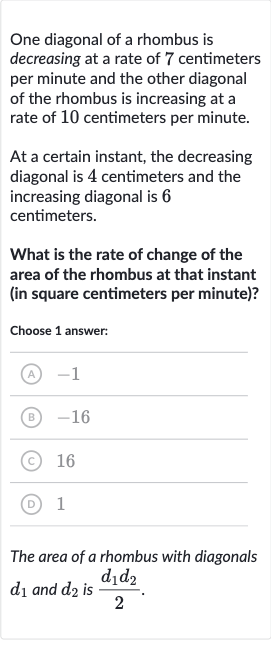
One diagonal of a rhombus is decreasing at a rate of $7$ centimeters per minute and the other diagonal of the rhombus is increasing at a rate of $10$ centimeters per minute. $\newline$ At a certain instant, the decreasing diagonal is $4$ centimeters and the increasing diagonal is $6$ centimeters. $\newline$ What is the rate of change of the area of the rhombus at that instant (in square centimeters per minute)? $\newline$ Choose $1$ answer: $\newline$ (A) $-1$ $\newline$ (B) $-16$ $\newline$ (C) $\mathbf{1 6}$ $\newline$ (D) $1$ $\newline$ The area of a rhombus with diagonals $d_{1}$ and $d_{2}$ is $\frac{d_{1} d_{2}}{2}$ .

Full solution

Q. One diagonal of a rhombus is decreasing at a rate of

7

centimeters per minute and the other diagonal of the rhombus is increasing at a rate of

10

centimeters per minute.

\newline

At a certain instant, the decreasing diagonal is

4

centimeters and the increasing diagonal is

6

centimeters.

\newline

What is the rate of change of the area of the rhombus at that instant (in square centimeters per minute)?

\newline

Choose

1

answer:

\newline

(A)

-1

\newline

(B)

-16

\newline

(C)

\mathbf{1 6}

\newline

(D)

1

\newline

The area of a rhombus with diagonals

d_{1}

and

d_{2}

\frac{d_{1} d_{2}}{2}

Rhombus Area Formula: The formula for the area of a rhombus is $(d_1 \times d_2) / 2$ , where $d_1$ and $d_2$ are the lengths of the diagonals.
Diagonal Lengths Given: Let's denote the decreasing diagonal as $d_1$ and the increasing diagonal as $d_2$ . At the instant we are considering, $d_1 = 4\,\text{cm}$ and $d_2 = 6\,\text{cm}$ .
Rates of Change: The rate of change of $d_1$ is $-7\,\text{cm/min}$ (since it's decreasing) and the rate of change of $d_2$ is $10\,\text{cm/min}$ (since it's increasing).
Rate of Change Formula: To find the rate of change of the area, we'll use the product rule for differentiation, which in this context is: $(\frac{dA}{dt}) = (d_1 \cdot (\frac{dd_2}{dt}) + d_2 \cdot (\frac{dd_1}{dt})) / 2$ .
Calculate Rate of Change: Plugging in the values we have: $(\frac{dA}{dt}) = \frac{(4 \, \text{cm} \times 10 \, \text{cm/min} + 6 \, \text{cm} \times -7 \, \text{cm/min})}{2}$ .
Perform Calculation: Now, let's do the calculation: $(\frac{dA}{dt}) = (\frac{40 \, \text{cm}^2/\text{min} - 42 \, \text{cm}^2/\text{min}}{2})$ .
Simplify Result: Simplifying that, we get: $(\frac{dA}{dt}) = \frac{-2 \, \text{cm}^2/\text{min}}{2}$ .
Final Rate of Change: Finally, we divide $-2\,\text{cm}^2/\text{min}$ by $2$ , which gives us $(\frac{dA}{dt}) = -1\,\text{cm}^2/\text{min}$ .