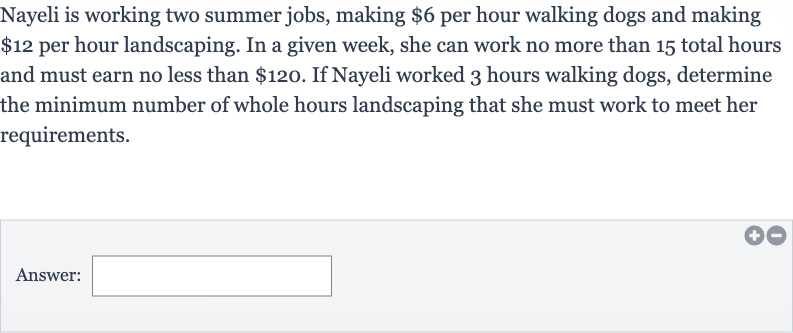
Nayeli is working two summer jobs, making $\$ 6$ per hour walking dogs and making $\$ 12$ per hour landscaping. In a given week, she can work no more than $15$ total hours and must earn no less than $\$ 120$ . If Nayeli worked $3$ hours walking dogs, determine the minimum number of whole hours landscaping that she must work to meet her requirements. $\newline$ Answer:

View step-by-step help

Home

Math Problems

Grade 7

GCF and LCM: word problems

Full solution

Q. Nayeli is working two summer jobs, making

\$ 6

per hour walking dogs and making

\$ 12

per hour landscaping. In a given week, she can work no more than

15

total hours and must earn no less than

\$ 120

. If Nayeli worked

3

hours walking dogs, determine the minimum number of whole hours landscaping that she must work to meet her requirements.

\newline

Answer:

Calculate Dog Walking Earnings: First, we need to calculate the amount Nayeli earns from walking dogs for $3$ hours. $\newline$ She makes $\$6$ per hour walking dogs. $\newline$ So, $3$ hours of dog walking would earn her $3$ hours * $\$6$ /hour = $\$18$ .
Subtract Dog Walking Earnings: Next, we need to subtract the amount earned from walking dogs from the total amount she needs to earn, which is $\$120$ . $\$120 - \$18 = \$102$ . Nayeli needs to earn at least $\$102$ from landscaping to meet her earnings requirement.
Calculate Landscaping Hours: Now, we calculate the number of hours she needs to work landscaping to earn $\$102$ . She makes $\$12$ per hour landscaping. So, the number of hours needed is $\$102 / \$12/\text{hour} = 8.5$ hours. Since she cannot work half hours, we round up to the nearest whole hour.
Check Total Hours Worked: Nayeli must work at least $9$ whole hours landscaping to meet her earnings requirement. $\newline$ However, we must also ensure that the total hours worked in both jobs do not exceed $15$ hours.
Check Total Hours Worked: Nayeli must work at least $9$ whole hours landscaping to meet her earnings requirement. $\newline$ However, we must also ensure that the total hours worked in both jobs do not exceed $15$ hours.We add the hours worked walking dogs to the hours needed for landscaping to check if it exceeds the $15$ -hour limit. $\newline$ $3$ hours (dog walking) + $9$ hours (landscaping) = $12$ hours. $\newline$ This does not exceed the $15$ -hour limit, so it is a valid solution.