Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

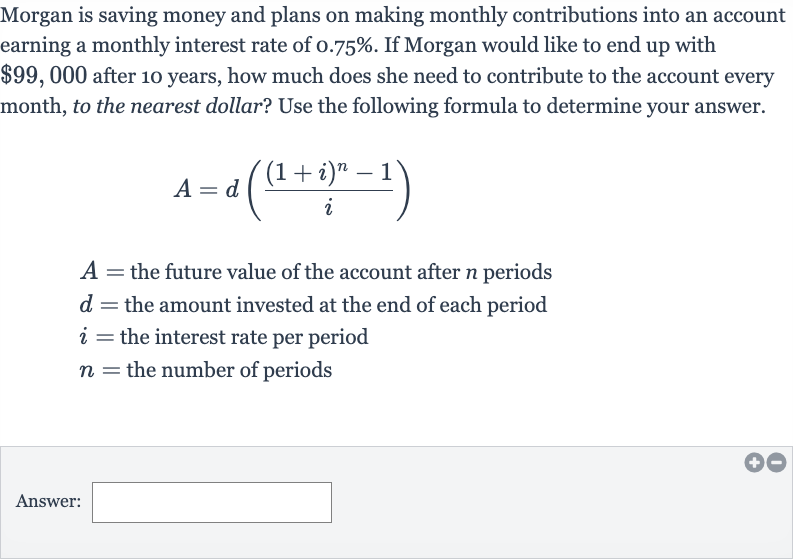
Morgan is saving money and plans on making monthly contributions into an account earning a monthly interest rate of 0.75%. If Morgan would like to end up with $99,000 after 10 years, how much does she need to contribute to the account every month, to the nearest dollar? Use the following formula to determine your answer. A=d(((1+i)^(n)-1)/(i)) A= the future value of the account after n periods d= the amount invested at the end of each period i= the interest rate per period n= the number of periods Answer:

Morgan is saving money and plans on making monthly contributions into an account earning a monthly interest rate of 0.75% 0.75 \% . If Morgan would like to end up with $99,000 \$ 99,000 after 1010 years, how much does she need to contribute to the account every month, to the nearest dollar? Use the following formula to determine your answer.\newlineA=d((1+i)n−1i) A=d\left(\frac{(1+i)^{n}-1}{i}\right) \newlineA= A= the future value of the account after n n periods\newlined= d= the amount invested at the end of each period\newlinei= i= the interest rate per period\newlinen= n= the number of periods\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 7right chevron icon
Compound interestright chevron icon

Full solution

Q. Morgan is saving money and plans on making monthly contributions into an account earning a monthly interest rate of 0.75% 0.75 \% . If Morgan would like to end up with $99,000 \$ 99,000 after 1010 years, how much does she need to contribute to the account every month, to the nearest dollar? Use the following formula to determine your answer.\newlineA=d((1+i)n−1i) A=d\left(\frac{(1+i)^{n}-1}{i}\right) \newlineA= A= the future value of the account after n n periods\newlined= d= the amount invested at the end of each period\newlinei= i= the interest rate per period\newlinen= n= the number of periods\newlineAnswer:
  1. Identify Given Values: Identify the given values from the problem.\newlineAA (future value of the account) = $99,000\$99,000\newlineii (monthly interest rate) = 0.75%0.75\% or 0.00750.0075 when converted to decimal\newlinenn (number of periods in 1010 years, with monthly contributions) = 1010 years ∗* 1212 months/year = 120120 months
  2. Plug into Formula: Plug the given values into the formula to solve for dd (the amount invested at the end of each period).A=d×((1+i)n−1i)A = d \times \left(\frac{(1 + i)^{n} - 1}{i}\right)(\newline\)$99,000=d×((1+0.0075)120−10.0075)\$99,000 = d \times \left(\frac{(1 + 0.0075)^{120} - 1}{0.0075}\right)
  3. Calculate (1+i)n(1 + i)^{n}: Calculate the value of (1+i)n(1 + i)^{n}.(1+0.0075)120=(1.0075)120(1 + 0.0075)^{120} = (1.0075)^{120}
  4. Calculate ((1+i)n−1)((1 + i)^{n} - 1): Calculate the value of ((1+i)n−1)((1 + i)^{n} - 1).
    (1.0075)120−1(1.0075)^{120} - 1
  5. Calculate Denominator: Calculate the denominator of the formula ii. 0.00750.0075
  6. Calculate Entire Right Side: Calculate the entire right side of the equation, which is the expression for dd.d=inlinelatex199,000((1.0075)120−1)/0.0075d = \frac{inline_latex_199,000}{\left(\left(1.0075\right)^{120} - 1\right) / 0.0075}
  7. Compute Values: Use a calculator to compute the values.\newlined=$99,000((1.0075)120−1)/0.0075d = \frac{\$99,000}{((1.0075)^{120} - 1) / 0.0075}\newlined≈$99,000(2.039887307…−1)/0.0075d \approx \frac{\$99,000}{(2.039887307\ldots - 1) / 0.0075}\newlined≈$99,0001.039887307…/0.0075d \approx \frac{\$99,000}{1.039887307\ldots / 0.0075}\newlined≈$99,000138.6516409…d \approx \frac{\$99,000}{138.6516409\ldots}\newlined≈$714.14d \approx \$714.14
  8. Round Monthly Contribution: Round the monthly contribution to the nearest dollar. d≈$(714)d \approx \$(714)

More problems from Compound interest

Question
Johnny bought an oil painting originally priced at $80 but on sale for 5050% off. After 1010% sales tax, what was the total cost?\newline`$`____
Get tutor helpright-arrow

Posted 4 months ago

Question
It costs `$40` to buy 44 ironing boards. If the ironing boards all have the same price, how much does it cost to buy 11 ironing board? ` $`_____
Get tutor helpright-arrow

Posted 7 months ago

Question
Whitney buys a lamp online for $93\$93. If shipping and handling are an additional 10%10\% of the price, how much shipping and handling will Whitney pay? \newline $\$ _____\_\_\_\_\_
Get tutor helpright-arrow

Posted 8 months ago

Question
A 99-foot roll of plastic wrap costs $5.40\$5.40. What is the price per inch? \newline $\$ _____
Get tutor helpright-arrow

Posted 7 months ago

Question
A store purchased canoes for $300\$300 and sold them for $435\$435. What percentage is the mark-up? \newlineWrite your answer using a percent sign (%\%). \newline _____
Get tutor helpright-arrow

Posted 7 months ago

Question
A ceramic vase was originally priced at $100\$100 but went on sale for 50%50\% off. If Ernesto bought the ceramic vase and paid 12%12\% sales tax, how much did he pay in total? \newline $\$ ____
Get tutor helpright-arrow

Posted 7 months ago

Question
A 1212-foot roll of aluminum foil costs $7.20\$7.20. What is the price per inch?
Get tutor helpright-arrow

Posted 9 months ago

Question
A 1515-foot roll of paper towel costs $9.75\$9.75. What is the price per inch?
Get tutor helpright-arrow

Posted 7 months ago

Question
A 2020-foot roll of ribbon costs $8.00\$8.00. What is the price per inch?
Get tutor helpright-arrow

Posted 9 months ago

Question
A 66-foot roll of fabric costs $4.50\$4.50. What is the price per inch? \newline $\$ ______
Get tutor helpright-arrow

Posted 7 months ago

View all (77)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant