AI tutor
Full solution
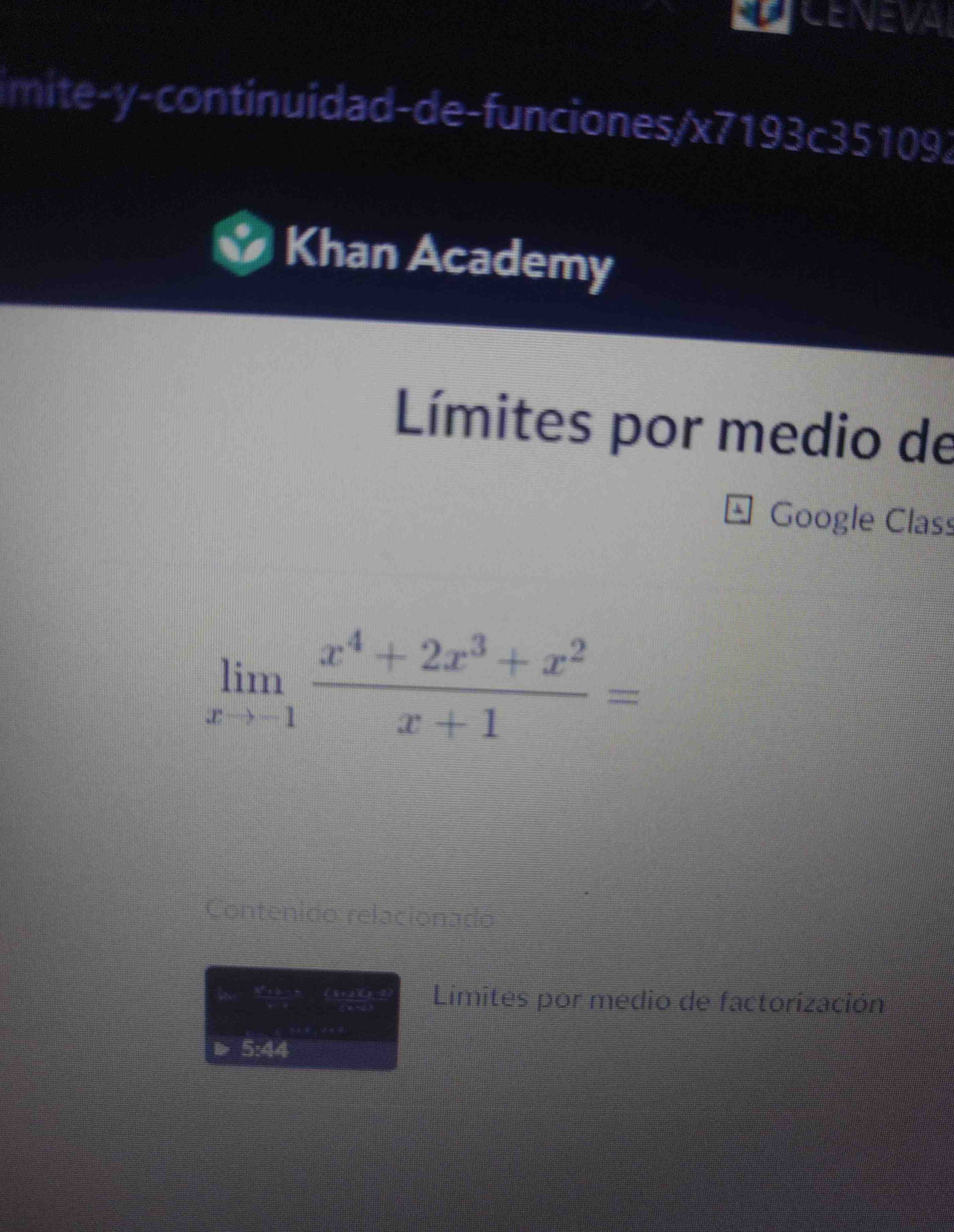
Q. Solve:
- Factorize Numerator: Step Title: Factorize the NumeratorConcise Step Description: Factorize the polynomial in the numerator.Step Calculation: Step Output:
- Simplify Expression: Step Title: Simplify the ExpressionConcise Step Description: Cancel out the common factor in the numerator and the denominator.Step Calculation: Step Output:
- Substitute Limit Value: Step Title: Substitute the Limit ValueConcise Step Description: Substitute into the simplified expression.Step Calculation: Step Output:
More problems from Factor polynomials
QuestionGet tutor help
QuestionGet tutor help