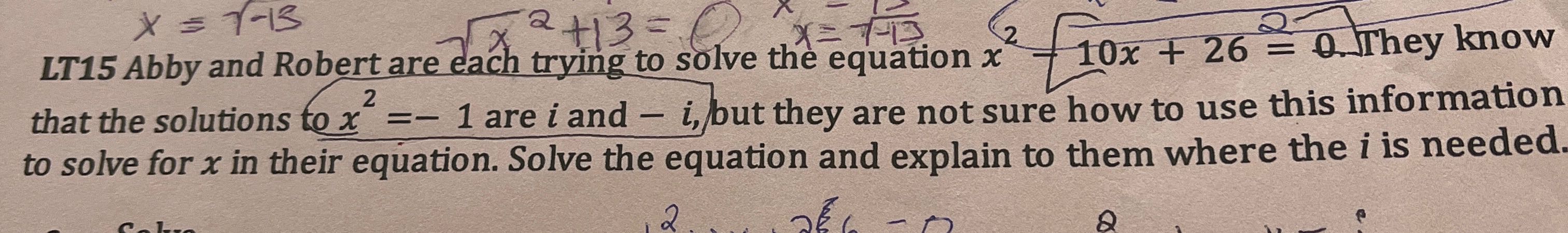Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Abby and Robert are each trying to solve the equation x^(2)-10 x+26=0. They know that the solutions to x^(2)=-1 are i and -i, but they are not sure how to use this information to solve for x in their equation. Solve the equation and explain to them where the i is needed.

Abby and Robert are each trying to solve the equation x2−10x+26=0x^{2}-10x+26=0. They know that the solutions to x2=−1x^{2}=-1 are ii and −i-i, but they are not sure how to use this information to solve for xx in their equation. Solve the equation and explain to them where the ii is needed.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Solve trigonometric equationsright chevron icon

Full solution

Q. Abby and Robert are each trying to solve the equation x2−10x+26=0x^{2}-10x+26=0. They know that the solutions to x2=−1x^{2}=-1 are ii and −i-i, but they are not sure how to use this information to solve for xx in their equation. Solve the equation and explain to them where the ii is needed.
  1. Rewrite Equation: Step 11: Rewrite the equation to isolate the square root term.\newlinex2−10x+26=0x^2 - \sqrt{10x + 26} = 0\newline⇒10x+26=x2\Rightarrow \sqrt{10x + 26} = x^2
  2. Square Both Sides: Step 22: Square both sides to eliminate the square root.\newline(10x+26)2=(x2)2(\sqrt{10x + 26})^2 = (x^2)^2\newline⇒10x+26=x4\Rightarrow 10x + 26 = x^4
  3. Rearrange Polynomial: Step 33: Rearrange the equation to form a standard polynomial equation. x4−10x−26=0x^4 - 10x - 26 = 0
  4. Factorize or Find Roots: Step 44: Attempt to factorize the polynomial or use a numerical method to find roots.\newlineThis polynomial is not easily factorizable, so numerical methods or graphing might be needed to find the roots.
  5. Check Imaginary Roots: Step 55: Check if any roots are imaginary.\newlineSince the original equation involved squaring both sides, we need to check if any solutions involve imaginary numbers. However, the polynomial x4−10x−26=0x^4 - 10x - 26 = 0 does not directly suggest imaginary roots without further analysis or numerical solution.

More problems from Solve trigonometric equations

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 1 month ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 1 month ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 2 months ago

View all (143)