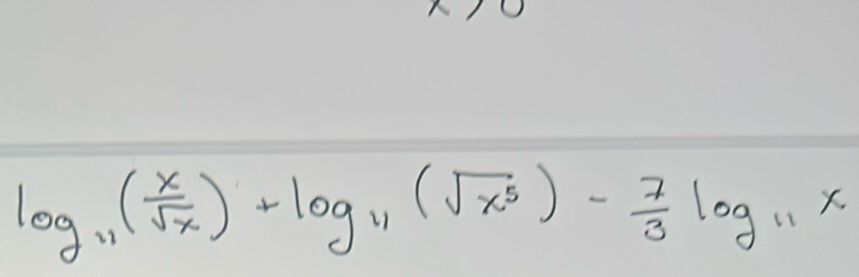Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

log_(11)((x)/(sqrtx))+log_(11)(sqrt(x^(5)))-(7)/(3)log_(11)x

$\log _{11}\left(\frac{x}{\sqrt{x}}\right)+\log _{11}\left(\sqrt{x^{5}}\right)-\frac{7}{3} \log _{11} x$

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q.

\log _{11}\left(\frac{x}{\sqrt{x}}\right)+\log _{11}\left(\sqrt{x^{5}}\right)-\frac{7}{3} \log _{11} x

Simplify logarithm expression: First, simplify $\log_{11}\left(\frac{x}{\sqrt{x}}\right)$ . Using the quotient rule of logarithms, $\log_b\left(\frac{a}{c}\right) = \log_b(a) - \log_b(c)$ , we get: $\log_{11}(x) - \log_{11}(\sqrt{x})$ . Since $\sqrt{x} = x^{1/2}$ , rewrite the expression: $\log_{11}(x) - \log_{11}(x^{1/2})$ . Using the power rule, $\log_b(a^c) = c\cdot\log_b(a)$ , we have: $\log_{11}(x) - \left(\frac{1}{2}\right)\cdot\log_{11}(x)$ . Simplify further: $\left(1 - \frac{1}{2}\right) \cdot \log_{11}(x) = \left(\frac{1}{2}\right) \cdot \log_{11}(x)$ .
Rewrite and simplify: Next, simplify $\log_{11}(\sqrt{x^{5}})$ . Rewrite $\sqrt{x^{5}}$ as $(x^{5})^{\frac{1}{2}} = x^{\frac{5}{2}}$ . Using the power rule: $\log_{11}(x^{\frac{5}{2}}) = \frac{5}{2} \cdot \log_{11}(x)$ .
Combine results and simplify: Combine the results from the previous steps: $\newline$ $(\frac{1}{2}) \cdot \log_{11}(x) + (\frac{5}{2}) \cdot \log_{11}(x) - (\frac{7}{3}) \cdot \log_{11}(x)$ . $\newline$ Combine like terms: $\newline$ $(\frac{1}{2} + \frac{5}{2} - \frac{7}{3}) \cdot \log_{11}(x)$ . $\newline$ Convert fractions to a common denominator and simplify: $\newline$ $(\frac{3}{6} + \frac{15}{6} - \frac{14}{6}) \cdot \log_{11}(x) = (\frac{4}{6}) \cdot \log_{11}(x)$ . $\newline$ Simplify the fraction: $\newline$ $(\frac{2}{3}) \cdot \log_{11}(x)$ .

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 2 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 1 month ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 2 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 1 month ago

Question

\newline

32^{(-1/5)}

Posted 1 month ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 1 month ago