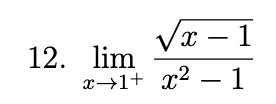Evaluate lim_(x rarr1^(+))(sqrt(x-1))/(x^(2)-1)

Question

Evaluate   lim_(x rarr1^(+))(sqrt(x-1))/(x^(2)-1)

Bytelearn · Accepted Answer

Understand the problem: Understand the problem. We need to find the limit of the function sqrt(x-1)/(x^2-1) as x approaches 1 from the right (denoted as x -> 1^+).Identify the form: Identify the form of the limit. Substitute x = 1 into the function to see if the limit can be directly calculated. lim_(x -> 1^+)(sqrt(x-1))/(x^2-1) = (sqrt(1-1))/(1^2-1) = 0/0 This is an indeterminate form, so we cannot directly calculate the limit.Simplify the denominator: Simplify the denominator. Notice that x^2 - 1 is a difference of squares, which can be factored as (x - 1)(x + 1).Analyze for simplification: Analyze the function for simplification. We can't directly simplify the square root in the numerator with the factors in the denominator. However, we can multiply the numerator and denominator by the conjugate of the numerator to remove the square root.Multiply by the conjugate: Multiply by the conjugate. Multiply the numerator and denominator by the conjugate of the numerator, which is sqrt(x-1). lim_(x -> 1^+)(sqrt(x-1))/(x^2-1) * (sqrt(x-1))/(sqrt(x-1))Perform the multiplication: Perform the multiplication. After multiplying, we get: lim_(x -> 1^+)(x-1)/(x^2-1)(sqrt(x-1))Simplify the expression: Simplify the expression. Now we can cancel out (x-1) from the numerator and denominator. lim_(x -> 1^+)(1)/((x+1)(sqrt(x-1)))Evaluate the limit: Evaluate the limit. Now that the expression is simplified, we can substitute x = 1 to find the limit. lim_(x -> 1^+)(1)/((1+1)(sqrt(1-1))) = 1/(2*0) This expression seems to suggest a division by zero, which is undefined. However, we must remember that we are taking the limit as x approaches 1 from the right, not at x = 1. Therefore, sqrt(x-1) is a small positive number, not zero.Conclude the limit: Conclude the limit. As x approaches 1 from the right, sqrt(x-1) approaches 0, and the denominator approaches 0. The limit of a function as the denominator approaches 0 from the positive side is +∞. Therefore, the limit of the function as x approaches 1 from the right is +∞.

Evaluate $\lim_{x \to 1^{+}}\left(\frac{\sqrt{x-1}}{x^{2}-1}\right)$

Full solution

More problems from Domain and range of square root functions: equations

Related topics

Evaluate lim⁡x→1+(x−1x2−1)\lim_{x \to 1^{+}}\left(\frac{\sqrt{x-1}}{x^{2}-1}\right)x→1+lim​(x2−1x−1​​)

Evaluate $\lim_{x \to 1^{+}}\left(\frac{\sqrt{x-1}}{x^{2}-1}\right)$