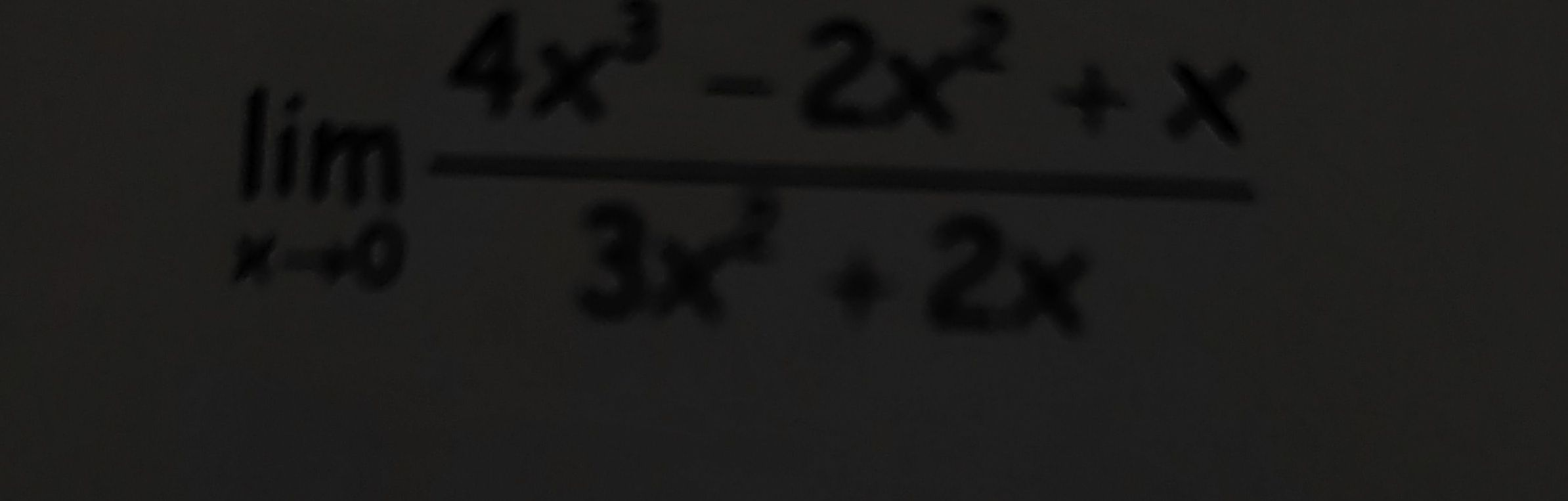AI tutor
Full solution
Q.
- Identify Problem Type: Identify the type of limit problem.We are dealing with a rational function where both the numerator and the denominator are polynomials. As approaches , both the numerator and the denominator approach , which is an indeterminate form . We need to simplify the expression or use L'Hôpital's Rule to find the limit.
- Simplify by Factoring: Simplify the expression by factoring if possible.We can factor out an from both the numerator and the denominator to simplify the expression.Now we can cancel out the common factor of from the numerator and the denominator, provided is not equal to .
- Evaluate Limit: Evaluate the limit of the simplified expression as approaches .Substitute into the simplified expression.
- State Final Answer: State the final answer.The limit of the function as approaches is .