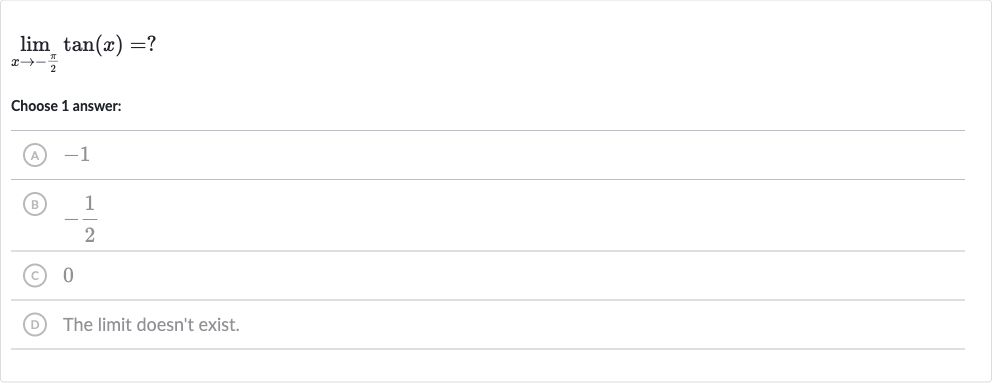
lim_(x rarr-(pi)/(2))tan(x)=? Choose 1 answer: (A) -1 (B) -(1)/(2) (C) 0 (D) The limit doesn't exist.

Question

lim_(x rarr-(pi)/(2))tan(x)=? Choose 1 answer: (A) -1 (B)  -(1)/(2) (C) 0 (D) The limit doesn't exist.

Bytelearn · Accepted Answer

Step 1: Determine the function and point of interest: We need to find the limit of the function tan(x) as x approaches -(pi)/(2). The tangent function has a period of pi, and it is known to have vertical asymptotes (where the function is undefined) at odd multiples of (pi)/2. Since -(pi)/(2) is one such point, we expect the limit to not exist because the tangent function approaches negative infinity from the right and positive infinity from the left of -(pi)/(2).Step 2: Analyze the behavior of sine and cosine functions: To confirm our expectation, we can consider the behavior of the sine and cosine functions separately, as tan(x) = sin(x)/cos(x). As x approaches -(pi)/(2), sin(x) approaches -1 and cos(x) approaches 0. The cosine function approaches 0 through positive values from the right of -(pi)/(2) and through negative values from the left of -(pi)/(2).Step 3: Observe the sign change of cosine function: Since the cosine function changes sign around -(pi)/(2), the tangent function will have opposite behaviors on either side of -(pi)/(2). From the right, tan(x) will approach negative infinity, and from the left, it will approach positive infinity. This confirms that the limit does not exist because the left-hand limit and the right-hand limit are not equal.Step 4: Determine the behavior of tangent function: Therefore, the correct answer is (D) The limit doesn't exist, because the function tan(x) does not approach a single finite value as x approaches -(pi)/(2).

$\lim _{x \rightarrow-\frac{\pi}{2}} \tan (x)=?$ $\newline$ Choose $1$ answer: $\newline$ (A) $-1$ $\newline$ (B) $-\frac{1}{2}$ $\newline$ (C) $0$ $\newline$ (D) The limit doesn't exist.

Full solution

More problems from Power rule

Related topics

lim⁡x→−π2tan⁡(x)=? \lim _{x \rightarrow-\frac{\pi}{2}} \tan (x)=? x→−2π​lim​tan(x)=?\newlineChoose 111 answer:\newline(A) −1-1−1\newline(B) −12 -\frac{1}{2} −21​\newline(C) 000\newline(D) The limit doesn't exist.

$\lim _{x \rightarrow-\frac{\pi}{2}} \tan (x)=?$ $\newline$ Choose $1$ answer: $\newline$ (A) $-1$ $\newline$ (B) $-\frac{1}{2}$ $\newline$ (C) $0$ $\newline$ (D) The limit doesn't exist.