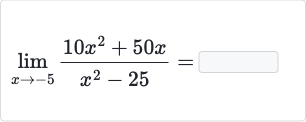AI tutor
Full solution
Q.
- Identify Function: Identify the function to find the limit of as approaches . We are given the function and we need to find its limit as approaches .
- Simplify Function: Simplify the function if possible.Notice that the numerator can be factored as . The denominator is a difference of squares and can be factored as .Simplified Form:
- Cancel Common Factors: Cancel out common factors.The term is common in both the numerator and the denominator, so we can cancel it out.After canceling:
- Substitute : Substitute with to find the limit.Now that we have simplified the function, we substitute with to find the limit.Limit:
- Perform Calculation: Perform the calculation.Calculate the limit using the values from the previous step.Limit: