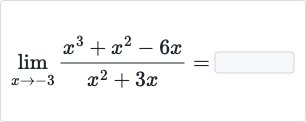AI tutor
Full solution
Q.
- Identify Function and Point: Identify the function and the point at which we need to find the limit.We are given the function and we need to find its limit as approaches .
- Simplify if Possible: Simplify the function if possible.We can factor both the numerator and the denominator to simplify the expression.Numerator: Denominator: Now we factor the quadratic in the numerator. can be factored into .So the function simplifies to:
- Cancel Common Factors: Cancel out common factors.We can cancel the common factor of and from the numerator and the denominator.This gives us:Which simplifies to:
- Find Limit: Find the limit by direct substitution.Now that we have simplified the function, we can find the limit by substituting with .