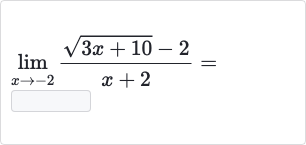AI tutor
Full solution
Q.
- Identify Indeterminate Form: Identify the indeterminate form.Substitute with in the function to see if it results in an indeterminate form.= This is an indeterminate form of type .
- Rationalize the Numerator: Rationalize the numerator.To resolve the indeterminate form, we can rationalize the numerator by multiplying the numerator and the denominator by the conjugate of the numerator.Conjugate of is .
- Apply Conjugate: Apply the conjugate.Multiply the numerators and the denominators.= = =
- Simplify the Expression: Simplify the expression.Notice that can be factored as .Now, we can cancel out the terms in the numerator and the denominator.
- Evaluate the Limit: Evaluate the limit.Now that the indeterminate form is resolved, substitute with .=
- Calculate Final Value: Calculate the final value. This is the final value of the limit as approaches .
More problems from Identify equivalent linear expressions I
QuestionGet tutor help