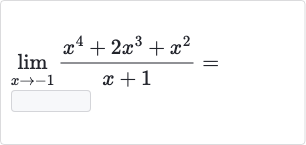lim_(x rarr-1)(x^(4)+2x^(3)+x^(2))/(x+1)=

Question

Bytelearn · Accepted Answer

Identify Function and Point: Identify the function and the point at which we need to find the limit. We are given the function f(x) = (x^4 + 2x^3 + x^2) / (x + 1) and we need to find the limit as x approaches -1.Check Indeterminate Form: Check if direct substitution of x = -1 into the function yields an indeterminate form. f(-1) = ((-1)^4 + 2(-1)^3 + (-1)^2) / (-1 + 1)        = (1 - 2 + 1) / 0        = 0/0 This is an indeterminate form, so we cannot simply substitute x = -1 to find the limit.Factor Numerator: Factor the numerator to simplify the expression. The numerator is a polynomial that can be factored by grouping. x^4 + 2x^3 + x^2 = x^2(x^2 + 2x + 1) Notice that x^2 + 2x + 1 is a perfect square trinomial and can be factored further. x^2(x^2 + 2x + 1) = x^2(x + 1)^2Cancel Common Factor: Cancel out the common factor from the numerator and the denominator. The common factor is (x + 1), which can be canceled out. f(x) = x^2(x + 1)^2 / (x + 1) After canceling out (x + 1), we get: f(x) = x^2(x + 1)Substitute and Find Limit: Substitute x = -1 into the simplified function to find the limit. f(-1) = (-1)^2(-1 + 1)        = 1(0)        = 0

$\lim _{x \rightarrow-1} \frac{x^{4}+2 x^{3}+x^{2}}{x+1}=$

Full solution

More problems from Negative Exponents

Related topics

lim⁡x→−1x4+2x3+x2x+1= \lim _{x \rightarrow-1} \frac{x^{4}+2 x^{3}+x^{2}}{x+1}= limx→−1​x+1x4+2x3+x2​=

$\lim _{x \rightarrow-1} \frac{x^{4}+2 x^{3}+x^{2}}{x+1}=$