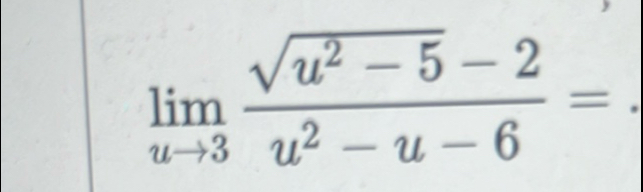lim_(u rarr3)(sqrt(u^(2)-5)-2)/(u^(2)-u-6)=

Question

Bytelearn · Accepted Answer

Factor Denominator: We are asked to find the limit of the function (sqrt(u^2 - 5) - 2) / (u^2 - u - 6) as u approaches 3. Let's first simplify the denominator and see if we can factor it. The denominator u^2 - u - 6 can be factored into (u - 3)(u + 2).Rewrite Limit Expression: Now that we have factored the denominator, let's rewrite the limit expression with the factored denominator: lim_(u -> 3)(sqrt(u^2 - 5) - 2) / ((u - 3)(u + 2)).Rationalize Numerator: We notice that if we substitute u = 3 directly into the limit expression, the denominator becomes 0, which would make the expression undefined. However, the numerator also becomes 0, as sqrt(3^2 - 5) - 2 = sqrt(4) - 2 = 2 - 2 = 0. This indicates that we may have a 0/0 indeterminate form, which suggests we should try to simplify the expression further or use L'Hôpital's Rule.Perform Multiplication: Before applying L'Hôpital's Rule, let's see if we can simplify the expression by rationalizing the numerator. We multiply the numerator and the denominator by the conjugate of the numerator, which is (sqrt(u^2 - 5) + 2): lim_(u -> 3)((sqrt(u^2 - 5) - 2)(sqrt(u^2 - 5) + 2)) / ((u - 3)(u + 2)(sqrt(u^2 - 5) + 2)).Cancel Terms: Now, let's perform the multiplication in the numerator, which is a difference of squares: (sqrt(u^2 - 5) - 2)(sqrt(u^2 - 5) + 2) = (u^2 - 5) - (2^2) = u^2 - 5 - 4 = u^2 - 9.Substitute and Simplify: The limit expression now becomes: lim_(u -> 3)(u^2 - 9) / ((u - 3)(u + 2)(sqrt(u^2 - 5) + 2)). We can now cancel out the (u - 3) term in the numerator and the denominator since u^2 - 9 can be factored into (u - 3)(u + 3): lim_(u -> 3)(u + 3) / ((u + 2)(sqrt(u^2 - 5) + 2)).Now we can substitute u = 3 into the simplified limit expression: lim_(u -> 3)(u + 3) / ((u + 2)(sqrt(u^2 - 5) + 2)) = (3 + 3) / ((3 + 2)(sqrt(3^2 - 5) + 2)).Perform the substitution and simplify the expression: (3 + 3) / ((3 + 2)(sqrt(3^2 - 5) + 2)) = 6 / ((5)(sqrt(9 - 5) + 2)) = 6 / (5 * (sqrt(4) + 2)) = 6 / (5 * (2 + 2)) = 6 / (5 * 4) = 6 / 20 = 3 / 10.

$\lim _{u \rightarrow 3} \frac{\sqrt{u^{2}-5}-2}{u^{2}-u-6}=$

Full solution

More problems from Find trigonometric ratios using reference angles

Related topics

lim⁡u→3u2−5−2u2−u−6= \lim _{u \rightarrow 3} \frac{\sqrt{u^{2}-5}-2}{u^{2}-u-6}= limu→3​u2−u−6u2−5​−2​=

$\lim _{u \rightarrow 3} \frac{\sqrt{u^{2}-5}-2}{u^{2}-u-6}=$