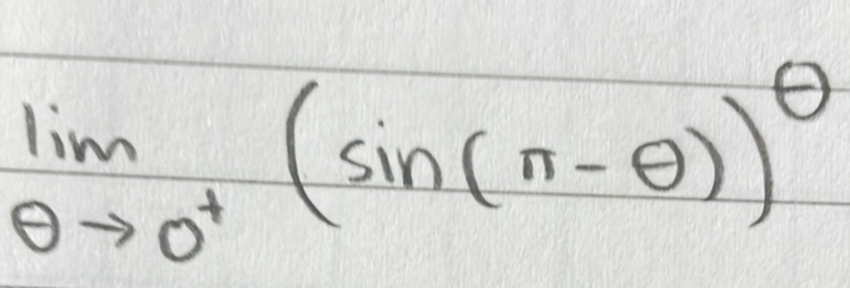$\lim _{\theta \rightarrow 0^{+}}(\sin (\pi-\theta))^{\theta}$

View step-by-step help

Home

Math Problems

Algebra 2

Csc, sec, and cot of special angles

Full solution

\lim _{\theta \rightarrow 0^{+}}(\sin (\pi-\theta))^{\theta}

Recognize symmetry of sine function: To solve the limit $\lim_{\theta\to 0^+}(\sin(\pi - \theta))^\theta$ , we first need to recognize that $\sin(\pi - \theta)$ is equivalent to $\sin(\theta)$ due to the symmetry of the sine function.
Rewrite expression with limit: Since $\sin(\theta)$ is continuous and differentiable at $\theta = 0$ , and $\sin(0) = 0$ , we can rewrite the expression as $(\sin(\theta))^\theta$ .
Apply exponential and logarithmic functions: We can now apply the limit to the expression. However, the direct substitution of $\theta = 0$ would result in the indeterminate form $0^0$ . To resolve this, we can use the exponential and logarithmic functions to transform the expression.
Take natural logarithm of expression: Let's set $y = (\sin(\theta))^\theta$ and take the natural logarithm of both sides to get $\ln(y) = \theta\ln(\sin(\theta))$ .
Apply L'Hôpital's Rule: Now we can find the limit of $\ln(y)$ as $\theta$ approaches $0$ from the positive side: $\lim_{\theta\to 0^+}\theta\ln(\sin(\theta))$ .
Evaluate limit of cotangent function: We can use L'Hôpital's Rule to evaluate this limit because it is in the indeterminate form $0*(-\infty)$ . Differentiate the numerator and the denominator with respect to $\theta$ .
Limit of natural logarithm is infinity: The derivative of the numerator $\ln(\sin(\theta))$ with respect to $\theta$ is $\frac{1}{\sin(\theta)} \cdot \cos(\theta) = \cot(\theta)$ , and the derivative of the denominator $\theta$ with respect to $\theta$ is $1$ .
Limit does not exist: Applying L'Hôpital's Rule, we get $\lim_{\theta\to 0^+}\frac{\cot(\theta)}{1}$ , which simplifies to $\lim_{\theta\to 0^+}\cot(\theta)$ .
Limit does not exist: Applying L'Hôpital's Rule, we get $\lim_{\theta\to 0^+}\frac{\cot(\theta)}{1}$ , which simplifies to $\lim_{\theta\to 0^+}\cot(\theta)$ .As $\theta$ approaches $0$ from the positive side, $\cot(\theta)$ approaches infinity. Therefore, the limit of $\ln(y)$ as $\theta$ approaches $0$ from the positive side is infinity.
Limit does not exist: Applying L'Hôpital's Rule, we get $\lim_{\theta\to 0^+}\frac{\cot(\theta)}{1}$ , which simplifies to $\lim_{\theta\to 0^+}\cot(\theta)$ .As $\theta$ approaches $0$ from the positive side, $\cot(\theta)$ approaches infinity. Therefore, the limit of $\ln(y)$ as $\theta$ approaches $0$ from the positive side is infinity.Since the limit of $\ln(y)$ is infinity, the limit of $y = e^{\ln(y)}$ is $\lim_{\theta\to 0^+}\cot(\theta)$ $0$ , which means the original limit $\lim_{\theta\to 0^+}\cot(\theta)$ $1$ is $\lim_{\theta\to 0^+}\cot(\theta)$ $0$ .
Limit does not exist: Applying L'Hôpital's Rule, we get $\lim_{\theta\to 0^+}\frac{\cot(\theta)}{1}$ , which simplifies to $\lim_{\theta\to 0^+}\cot(\theta)$ .As $\theta$ approaches $0$ from the positive side, $\cot(\theta)$ approaches infinity. Therefore, the limit of $\ln(y)$ as $\theta$ approaches $0$ from the positive side is infinity.Since the limit of $\ln(y)$ is infinity, the limit of $y = e^{\ln(y)}$ is $\lim_{\theta\to 0^+}\cot(\theta)$ $0$ , which means the original limit $\lim_{\theta\to 0^+}\cot(\theta)$ $1$ is $\lim_{\theta\to 0^+}\cot(\theta)$ $0$ .However, $\lim_{\theta\to 0^+}\cot(\theta)$ $0$ is not a finite number; it represents that the function grows without bound. Therefore, the limit does not exist in the real number system.