AI tutor
Full solution
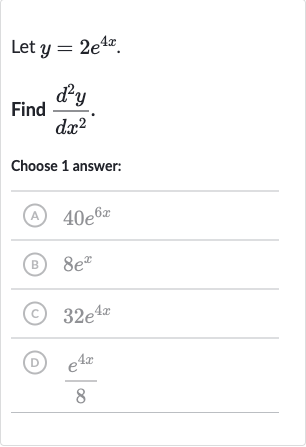
Q. Let .Find .Choose answer:(A) (B) (C) (D)
- Find First Derivative: Differentiate the function with respect to to find the first derivative.Using the chain rule, the derivative of is , and since we have a constant multiplied, the first derivative is:
- Apply Chain Rule: Differentiate the first derivative to find the second derivative.Again using the chain rule, the derivative of is , which gives us: