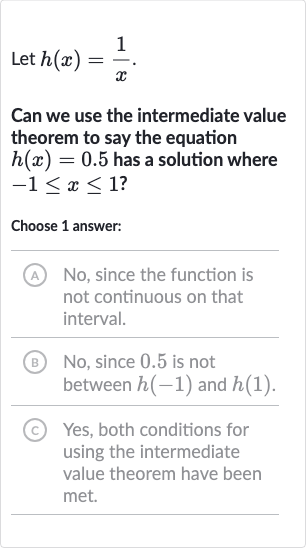
Let $h(x)=\frac{1}{x}$ . $\newline$ Can we use the intermediate value theorem to say the equation $h(x)=0.5$ has a solution where $-1 \leq x \leq 1$ ? $\newline$ Choose $1$ answer: $\newline$ (A) No, since the function is not continuous on that interval. $\newline$ (B) No, since $0$ . $5$ is not between $h(-1)$ and $h(1)$ . $\newline$ (C) Yes, both conditions for using the intermediate value theorem have been met.

Full solution

Q. Let

h(x)=\frac{1}{x}

\newline

Can we use the intermediate value theorem to say the equation

h(x)=0.5

has a solution where

-1 \leq x \leq 1

\newline

Choose

1

answer:

\newline

(A) No, since the function is not continuous on that interval.

\newline

(B) No, since

0

5

is not between

h(-1)

and

h(1)

\newline

Theorem Statement: The intermediate value theorem states that if a function $f$ is continuous on a closed interval $[a, b]$ and $k$ is any number between $f(a)$ and $f(b)$ , then there exists at least one number $c$ in the interval $[a, b]$ such that $f(c) = k$ .
Check Continuity: First, we need to check if the function $h(x) = \frac{1}{x}$ is continuous on the interval $[-1, 1]$ . We know that $h(x)$ is not defined at $x = 0$ , which lies within the interval $[-1, 1]$ . Therefore, $h(x)$ is not continuous on the entire interval $[-1, 1]$ because of the discontinuity at $x = 0$ .
Use of Theorem: Since $h(x)$ is not continuous on the interval $[-1, 1]$ , we cannot use the intermediate value theorem to say that the equation $h(x) = 0.5$ has a solution on that interval.