Let $g(x)=\frac{x}{\ln (x-2)}$ . $\newline$ Select the correct description of the one-sided limits of $g$ at $x=3$ . $\newline$ Choose $1$ answer: $\newline$ (A) $\lim _{x \rightarrow 3^{+}} g(x)=+\infty$ and $\lim _{x \rightarrow 3^{-}} g(x)=+\infty$ $\newline$ (B) $\lim _{x \rightarrow 3^{+}} g(x)=+\infty$ and $\lim _{x \rightarrow 3^{-}} g(x)=-\infty$ $\newline$ (C) $\lim _{x \rightarrow 3^{+}} g(x)=-\infty$ and $\lim _{x \rightarrow 3^{-}} g(x)=+\infty$ $\newline$ (D) $\lim _{x \rightarrow 3^{+}} g(x)=-\infty$ and $\lim _{x \rightarrow 3^{-}} g(x)=-\infty$

Full solution

Q. Let

g(x)=\frac{x}{\ln (x-2)}

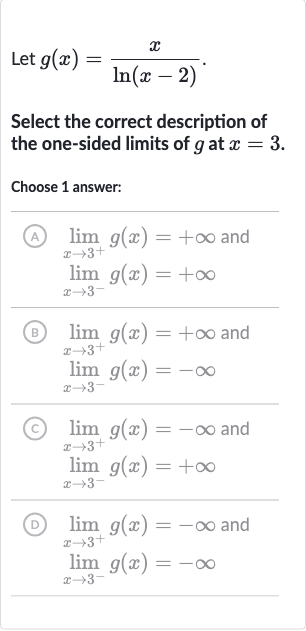
\newline

Select the correct description of the one-sided limits of

g

x=3

\newline

Choose

1

answer:

\newline

(A)

\lim _{x \rightarrow 3^{+}} g(x)=+\infty

and

\lim _{x \rightarrow 3^{-}} g(x)=+\infty

\newline

(B)

\lim _{x \rightarrow 3^{+}} g(x)=+\infty

and

\lim _{x \rightarrow 3^{-}} g(x)=-\infty

\newline

(C)

\lim _{x \rightarrow 3^{+}} g(x)=-\infty

and

\lim _{x \rightarrow 3^{-}} g(x)=+\infty

\newline

(D)

\lim _{x \rightarrow 3^{+}} g(x)=-\infty

and

\lim _{x \rightarrow 3^{-}} g(x)=-\infty

Understand the Function: Understand the function and the point of interest. $\newline$ We are given the function $g(x) = \frac{x}{\ln(x-2)}$ and we need to find the one-sided limits as $x$ approaches $3$ from the right ( $x \to 3^+$ ) and from the left ( $x \to 3^-$ ).
Analyze Right Approach: Analyze the behavior of the function as $x$ approaches $3$ from the right ( $x \to 3^+$ ). $\newline$ As $x$ approaches $3$ from the right, the numerator $x$ approaches $3$ , and the denominator $\ln(x-2)$ approaches $\ln(3-2)$ which is $\ln(1) = 0$ . Since the natural logarithm of a number very close to $3$ $0$ from the right is a very small positive number, the fraction $3$ $1$ will approach positive infinity. $\newline$ $3$ $2$
Analyze Left Approach: Analyze the behavior of the function as $x$ approaches $3$ from the left ( $x \to 3^-$ ). $\newline$ As $x$ approaches $3$ from the left, the numerator $x$ approaches $3$ , and the denominator $\ln(x-2)$ approaches $\ln(3-2)$ which is $\ln(1) = 0$ . However, since we are approaching from the left, $3$ $0$ is slightly less than $3$ $1$ , and the natural logarithm of a number slightly less than $3$ $1$ is negative and approaches negative infinity. Therefore, the fraction $3$ $3$ will approach negative infinity. $\newline$ $3$ $4$