Full solution
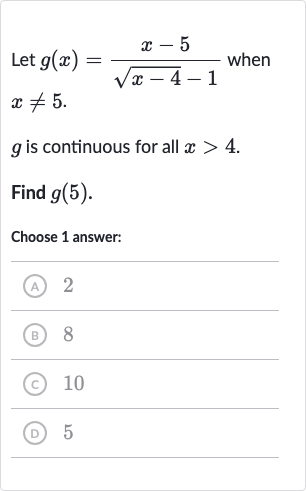
Q. Let when . is continuous for all .Find .Choose answer:(A) (B) (C) (D)
- Given function: We are given the function and we need to find the value of . However, we cannot directly substitute into the function because it would result in a division by zero, which is undefined. We need to find a way to simplify the function or use a limit approach to find the value of .
- Simplifying the function: To simplify the function, we can multiply the numerator and the denominator by the conjugate of the denominator to eliminate the square root. The conjugate of is .
- Multiplying by the conjugate: Multiplying the numerator and denominator by the conjugate, we get:g(x) =
- Simplifying the denominator: Simplifying the denominator using the difference of squares, we get:
- Canceling out terms: Further simplifying the denominator, we get:g(x) = ] / [x - ]\)
- Substituting : Now we can see that the terms in the numerator and denominator will cancel out, as long as . This gives us:
- Calculating the result: Since we have simplified the function and there is no longer a division by zero, we can now substitute into the simplified function to find :
- Calculating the result: Since we have simplified the function and there is no longer a division by zero, we can now substitute into the simplified function to find :
Calculating the square root and the addition, we get:
More problems from Domain and range of square root functions: equations
QuestionGet tutor help
QuestionGet tutor help