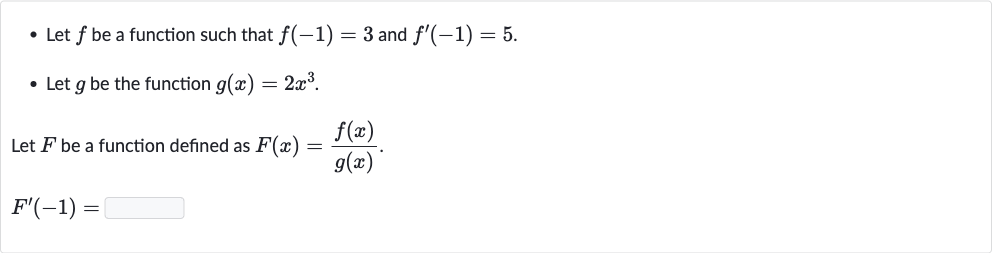Full solution
Q. - Let be a function such that and .- Let be the function .Let be a function defined as .
- Apply Quotient Rule: To find , we need to use the quotient rule for differentiation, which states that if , then . We are given and . We also have , so we need to find and .
- Find : First, let's find by substituting into :
- Find : Next, we need to find . To do this, we first differentiate with respect to :
Now we substitute into to find : - Apply Quotient Rule: Now we have all the values we need to apply the quotient rule:
- Simplify Numerator and Denominator: Let's simplify the numerator and the denominator separately:Numerator: Denominator:
- Find : Now we can find :