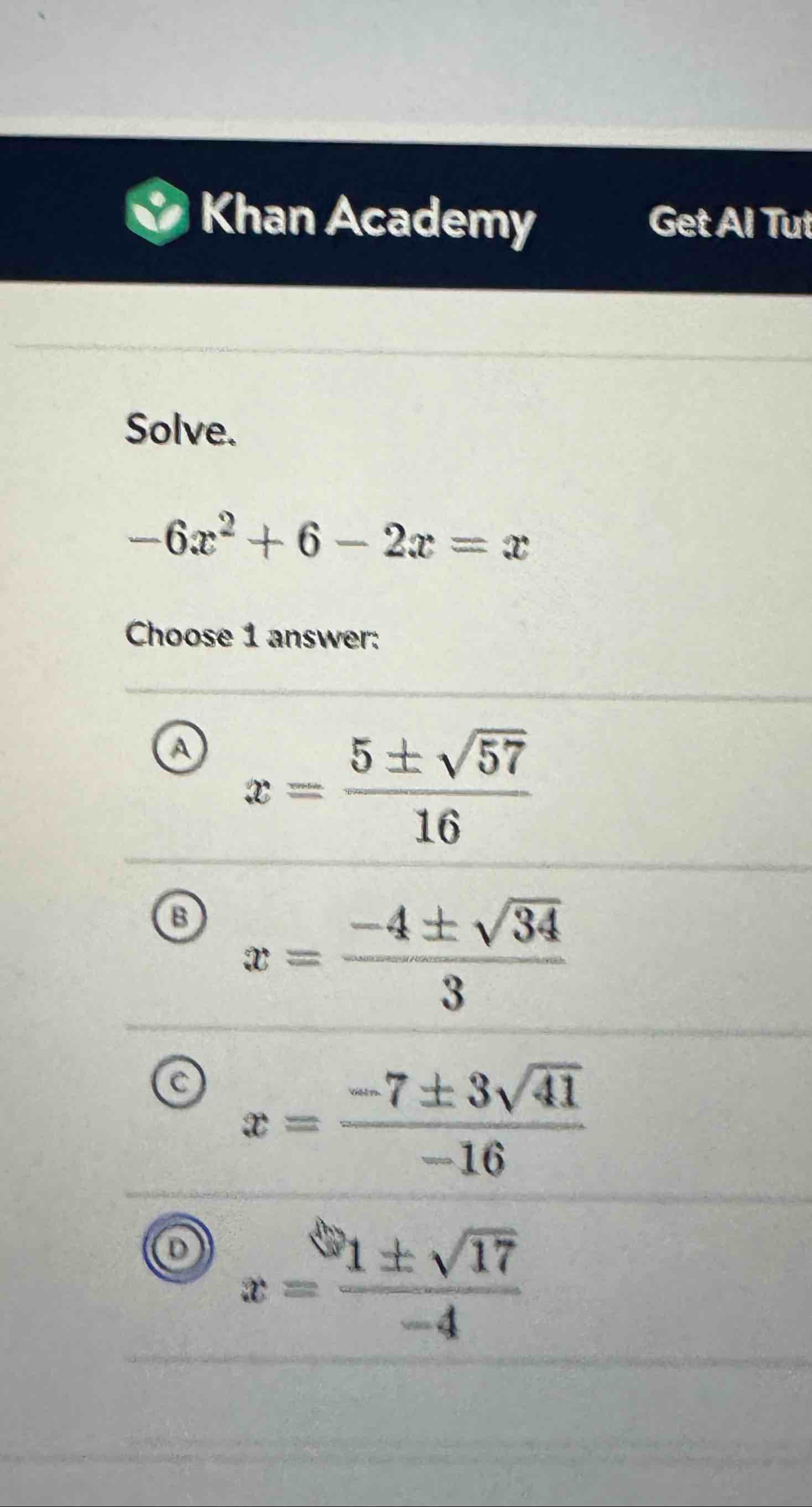
Solve. -6x^(2)+6-2x=x Choose 1 answer: (A) x=(5+-sqrt57)/(16) (B) x=(-4+-sqrt34)/(3) (C) x=(-7+-3sqrt41)/(-16) (D) x=(1+-sqrt17)/(-4)

Question

Bytelearn · Accepted Answer

Bring terms together: First, we need to bring all terms to one side of the equation to set it equal to zero. We do this by subtracting x from both sides of the equation. -6x^2 + 6 - 2x - x = 0 This simplifies to: -6x^2 - 3x + 6 = 0Solve quadratic equation: Next, we need to solve the quadratic equation. We can do this by using the quadratic formula, which is x = (-b ± √(b^2 - 4ac)) / (2a), where a, b, and c are the coefficients from the quadratic equation ax^2 + bx + c = 0. In our case, a = -6, b = -3, and c = 6.Plug values into formula: Now we will plug the values of a, b, and c into the quadratic formula. x = (-(-3) ± √((-3)^2 - 4(-6)(6))) / (2(-6)) This simplifies to: x = (3 ± √(9 + 144)) / (-12) x = (3 ± √153) / (-12)Simplify square root: We simplify √153 to get the exact values for x. √153 is not a perfect square, so we leave it as is. x = (3 ± √153) / (-12)Divide by common divisor: We can simplify the fraction by dividing the numerator and the denominator by their greatest common divisor, which is 3 in this case. x = (1 ± √(153)/3) / (-4) Since √(153)/3 is not a simplifiable square root, we leave it as is. x = (1 ± √(153)/3) / (-4)Match with answer choice: Now we look at the answer choices to see which one matches our result. We notice that √153 is the same as √(17*9), which simplifies to 3√17. So our equation becomes: x = (1 ± 3√17) / (-4) This matches answer choice (D).

Solve. $\newline$ $-6 x^{2}+6-2 x=x$ $\newline$ Choose $1$ answer: $\newline$ (A) $x=\frac{5 \pm \sqrt{57}}{16}$ $\newline$ (B) $x=\frac{-4 \pm \sqrt{34}}{3}$ $\newline$ (C) $x=\frac{-7 \pm 3 \sqrt{41}}{-16}$ $\newline$ (D) $x=\frac{1 \pm \sqrt{17}}{-4}$

Full solution

More problems from Sum of finite series starts from 1

Related topics