Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

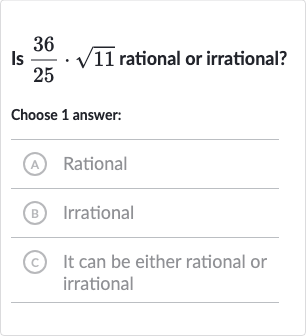
Is (36)/(25)*sqrt11 rational or irrational? Choose 1 answer: (A) Rational (B) Irrational C) It can be either rational or irrational

Is 3625⋅11\frac{36}{25} \cdot \sqrt{11} rational or irrational?\newlineChoose 11 answer:\newline(A) Rational\newline(B) Irrational\newline(C) It can be either rational or irrational

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Multiplication with rational exponentsright chevron icon

Full solution

Q. Is 3625⋅11\frac{36}{25} \cdot \sqrt{11} rational or irrational?\newlineChoose 11 answer:\newline(A) Rational\newline(B) Irrational\newline(C) It can be either rational or irrational
  1. Understand rational vs irrational: Understand the definition of rational and irrational numbers.\newlineA rational number is a number that can be expressed as the quotient or fraction pq\frac{p}{q} of two integers, where pp and qq are integers and qq is not zero. An irrational number cannot be expressed as a simple fraction; it's a number that cannot be written as a ratio of two integers.
  2. Analyze given expression: Analyze the given expression.\newlineThe expression is (3625)11(\frac{36}{25})\sqrt{11}. We know that 3636 and 2525 are integers, so (3625)(\frac{36}{25}) is a rational number. However, we need to determine the nature of 11\sqrt{11}.
  3. Determine 11\sqrt{11} nature: Determine the nature of 11\sqrt{11}. The square root of 1111, 11\sqrt{11}, is an irrational number because 1111 is not a perfect square, and its square root cannot be expressed as a fraction of two integers.
  4. Multiply rational by irrational: Multiply a rational number by an irrational number.\newlineWhen we multiply a rational number by an irrational number, the result is always an irrational number. This is because the irrational number cannot be expressed as a fraction, and multiplying by a fraction (rational number) does not change this fact.
  5. Conclude expression type: Conclude whether the expression is rational or irrational.\newlineSince (3625)(\frac{36}{25}) is rational and 11\sqrt{11} is irrational, their product (3625)⋅11(\frac{36}{25})\cdot\sqrt{11} is irrational.

More problems from Multiplication with rational exponents

Question
Simplify.\newline811281^{\frac{1}{2}}\newline_____________
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify.\newline(−32)1/5(-32)^{1/5}\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Assume all variables are positive.\newlinew43w73\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. Assume all variables are positive.\newline(2r13)8(2r^{\frac{1}{3}})^8\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. Assume all variables are positive.\newlinev74⋅v94v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify.\newline114⋅1141^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. \newline32(−1/5)32^{(-1/5)}
Get tutor helpright-arrow

Posted 7 months ago

Question
Simplify. Assume all variables are positive.\newlinew32w52\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Assume all variables are positive.\newline(27x)23(27x)^{\frac{2}{3}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 8 months ago

Question
Simplify. Assume all variables are positive.\newlinex14x114\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 7 months ago

View all (744)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant