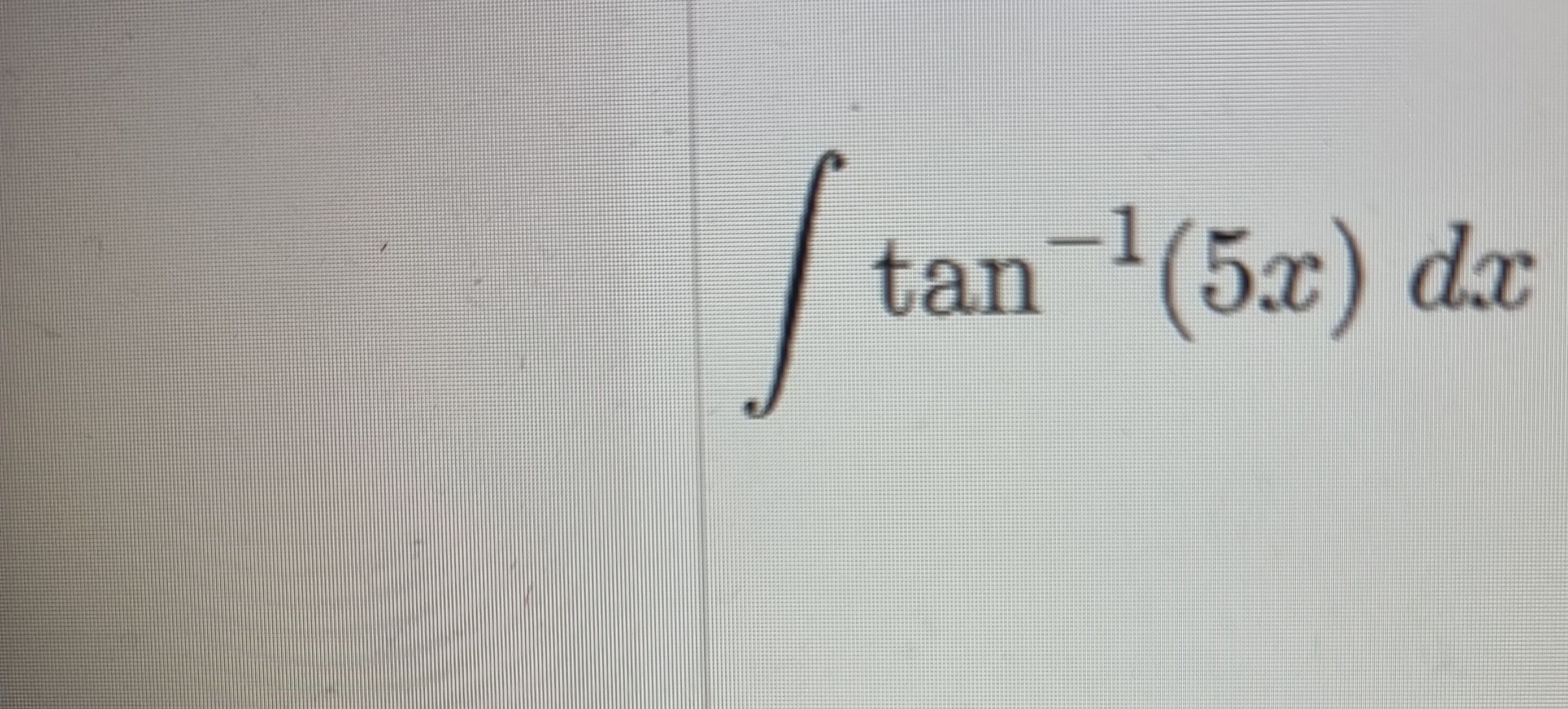AI tutor
Full solution
Q.
- Identify integral: Identify the integral that needs to be solved.We need to find the integral of the function with respect to .
- Use integration by parts: Use integration by parts.Integration by parts formula is , where and are parts of the integrand.Let , which means .Let , which means .
- Differentiate and integrate: Differentiate and integrate .\ Differentiate to find :\ \ Integrate to find :\
- Apply integration by parts: Apply the integration by parts formula.Now we have , , , and , we can apply the integration by parts formula:=
- Simplify the integral: Simplify the integral.We need to simplify the integral .Let's make a substitution to simplify this integral. Let , then .
- Change variables: Change the variables in the integral.Substitute and into the integral:We have the extra because , so we need to multiply by to get the original , and since we have a in the numerator, .
- Integrate with respect to : Integrate with respect to . Now integrate : \frac{\(1\)}{\(2\)} \times \int\left(\frac{\(5\)}{w}\right)dw = \frac{\(1\)}{\(2\)} \times \(5 \times \ln|w| + C = \left(\frac{}{}\right) \times \ln|w| + C
- Substitute back for x: Substitute back for x.Now we need to substitute back in for to get the integral in terms of :
- Combine integration results: Combine the results from integration by parts.Combine the result from Step and Step to get the final answer:
More problems from Evaluate integers raised to rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help