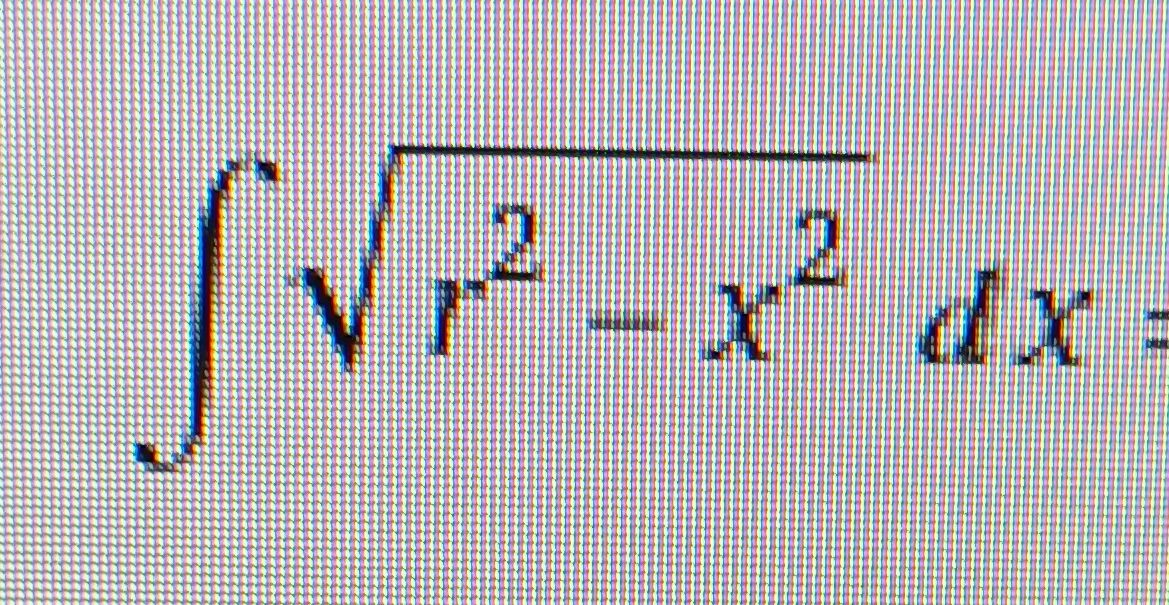intsqrt(r^(2)-x^(2))dx=

Question

Bytelearn · Accepted Answer

Recognize Trigonometric Substitution: To solve the integral ∫√(r^2 - x^2) dx, we recognize that this is a standard integral that can be solved using a trigonometric substitution. Specifically, we can let x = r sin(θ), which implies dx = r cos(θ) dθ. This substitution will simplify the square root expression.Substitute x into Integral: We substitute x = r sin(θ) into the integral, which gives us ∫√(r^2 - (r sin(θ))^2) r cos(θ) dθ. Simplifying the expression under the square root gives us ∫√(r^2(1 - sin^2(θ))) r cos(θ) dθ.Simplify Square Root Expression: We know that sin^2(θ) + cos^2(θ) = 1, so 1 - sin^2(θ) = cos^2(θ). Substituting this into the integral, we get ∫r cos(θ) * r cos(θ) dθ, which simplifies to ∫r^2 cos^2(θ) dθ.Integrate r^2 cos^2(θ): Now we need to integrate r^2 cos^2(θ) with respect to θ. This can be done by using the half-angle identity for cosine, which states that cos^2(θ) = (1 + cos(2θ))/2. Substituting this into the integral, we get ∫r^2 (1 + cos(2θ))/2 dθ.Split Integral into Two Parts: We can split the integral into two parts: ∫(r^2/2) dθ + ∫(r^2/2) cos(2θ) dθ. This simplifies the integration process.Use u-Substitution for cos(2θ): Integrating the first part, ∫(r^2/2) dθ, gives us (r^2/2)θ. For the second part, ∫(r^2/2) cos(2θ) dθ, we can use a u-substitution where u = 2θ and du = 2 dθ, which gives us (1/4)∫r^2 cos(u) du.Combine Results of Integrals: The integral of cos(u) with respect to u is sin(u), so we get (r^2/4)sin(u). Substituting back for u, we have (r^2/4)sin(2θ).Substitute back for θ: Combining the results from the two parts of the integral, we have (r^2/2)θ + (r^2/4)sin(2θ) + C, where C is the constant of integration.Find θ using Inverse Sine: We now need to substitute back for θ using our original substitution x = r sin(θ). To find θ, we take the inverse sine of both sides, giving us θ = arcsin(x/r).Substitute θ into Result: Substituting θ = arcsin(x/r) into our result, we get (r^2/2)arcsin(x/r) + (r^2/4)sin(2arcsin(x/r)) + C.Simplify sin(2arcsin(x/r)): To simplify sin(2arcsin(x/r)), we use the identity sin(2θ) = 2sin(θ)cos(θ). Since sin(θ) = x/r, we need to find cos(θ). From the Pythagorean identity, we know that cos(θ) = √(1 - sin^2(θ)) = √(1 - (x/r)^2).Finalize the Answer: Substituting sin(θ) = x/r and cos(θ) = √(1 - (x/r)^2) into sin(2θ), we get sin(2arcsin(x/r)) = 2(x/r)√(1 - (x/r)^2).Finally, we substitute sin(2arcsin(x/r)) back into our integral result to get the final answer: (r^2/2)arcsin(x/r) + (r^2/4)(2(x/r)√(1 - (x/r)^2)) + C.Simplifying the expression, we get (r^2/2)arcsin(x/r) + (r^2/2)(x/r)√(1 - (x/r)^2) + C as the final answer.

$\int \sqrt{r^{2}-x^{2}} d x=$

Full solution

More problems from Csc, sec, and cot of special angles

Related topics

∫r2−x2dx= \int \sqrt{r^{2}-x^{2}} d x= ∫r2−x2​dx=

$\int \sqrt{r^{2}-x^{2}} d x=$