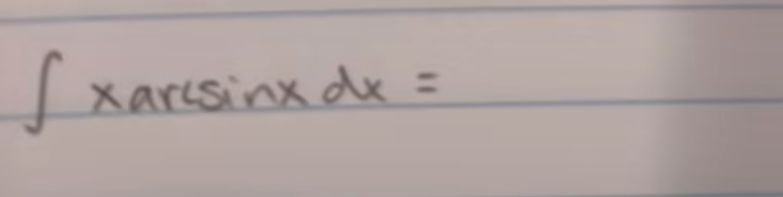$\int x \arcsin x d x=$

View step-by-step help

Home

Math Problems

Algebra 2

Csc, sec, and cot of special angles

Full solution

\int x \arcsin x d x=

Integration by Parts: To solve the integral of $x$ times the arcsin of $x$ , we can use integration by parts, which is based on the product rule for differentiation and is given by the formula: $\newline$ $\int u \, dv = uv - \int v \, du$ $\newline$ Here, we can let $u = \arcsin(x)$ and $dv = x \, dx$ . Then we need to find $du$ and $v$ .
Derivative of arcsin(x): First, we differentiate $u = \text{arcsin}(x)$ with respect to $x$ to find $du$ . The derivative of $\text{arcsin}(x)$ with respect to $x$ is $\frac{1}{\sqrt{1 - x^2}}$ . Therefore, $du = \left(\frac{1}{\sqrt{1 - x^2}}\right) dx$ .
Integral of $x$ : Next, we integrate $dv = x dx$ to find $v$ . The integral of $x$ with respect to $x$ is $(1/2)x^2$ . Therefore, $v = (1/2)x^2$ .
Apply integration by parts: Now we apply the integration by parts formula: $\newline$ $\int x \arcsin(x) \, dx = uv - \int v \, du$ $\newline$ = $(\arcsin(x))(\frac{1}{2})x^2 - \int((\frac{1}{2})x^2)(\frac{1}{\sqrt{1 - x^2}}) \, dx$
Simplify the integral: We simplify the integral on the right: $\newline$ $\int\left(\frac{1}{2}x^2\right)\left(\frac{1}{\sqrt{1 - x^2}}\right) dx$ $\newline$ = \frac{$1$}{$2$}\int\left(\frac{x^$2$}{\sqrt{$1$ - x^$2$}}\right) dx
Use substitution: This integral can be tricky, but we can use a substitution to simplify it. Let's use the substitution:\(\newlineLet $w = 1 - x^2$ , then $dw = -2x dx$ .
Solve for $x dx$ : We solve for $x dx$ in terms of $dw$ : $x dx = -\frac{dw}{2}$
Separate and integrate: Substitute $w$ and $x dx$ into the integral: $\frac{1}{2}\int\left(\frac{x^2}{\sqrt{1 - x^2}}\right) dx$ = $\frac{1}{2}\int\left(\frac{1 - w}{\sqrt{w}}\right) \left(-\frac{dw}{2}\right)$ = $-\frac{1}{4}\int\left(\frac{1 - w}{\sqrt{w}}\right) dw$
Integrate each term: Now we separate the integral into two parts and integrate each one: $\newline$ $-\frac{1}{4}\int\frac{(1 - w)}{\sqrt{w}} dw$ $\newline$ = $-\frac{1}{4}\int\frac{1}{\sqrt{w}} dw + \frac{1}{4}\int\frac{w}{\sqrt{w}} dw$ $\newline$ = -\frac{$1$}{$4$}\int w^{-\frac{$1$}{$2$}} dw + \frac{$1$}{$4$}\int w^{\frac{$1$}{$2$}} dw)
Combine and substitute: Integrate each term:\(\newline $-\frac{1}{4}\int(w^{-\frac{1}{2}}) dw = -\frac{1}{4}(2w^{\frac{1}{2}}) = -\frac{1}{2}\sqrt{w}$ $\newline$ $\frac{1}{4}\int(w^{\frac{1}{2}}) dw = \frac{1}{4}(\frac{2}{3})w^{\frac{3}{2}} = \frac{1}{6}w^{\frac{3}{2}}$
Final integral: Combine the two terms and substitute back for $w = 1 - x^2$ : $-\frac{1}{2}\sqrt{w} + \frac{1}{6}w^{\frac{3}{2}}$ = $-\frac{1}{2}\sqrt{1 - x^2} + \frac{1}{6}(1 - x^2)^{\frac{3}{2}}$
Simplify the expression: Now we have the integral we need to subtract from $uv$ : $\int x \arcsin(x) \, dx = (\arcsin(x))(\frac{1}{2})x^2 - \left(-\left(\frac{1}{2}\right)\sqrt{1 - x^2} + \left(\frac{1}{6}\right)(1 - x^2)^{\frac{3}{2}}\right) + C$
Simplify the expression: Now we have the integral we need to subtract from uv: $\newline$ $\int x \arcsin(x) dx = (\arcsin(x))(\frac{1}{2})x^2 - (-(\frac{1}{2})\sqrt{1 - x^2} + (\frac{1}{6})(1 - x^2)^{\frac{3}{2}}) + C$ Simplify the expression: $\newline$ $\int x \arcsin(x) dx = (\frac{1}{2})x^2 \arcsin(x) + (\frac{1}{2})\sqrt{1 - x^2} - (\frac{1}{6})(1 - x^2)^{\frac{3}{2}} + C$ $\newline$ This is the final answer in simplified form.