Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

$In /_\JKL,m/_J=(5x+1)^(@),m/_K=(x+14)^(@), and m/_L=(3x+12)^(@). What is the value of x ? Answer:$

In $\triangle \mathrm{JKL}, \mathrm{m} \angle J=(5 x+1)^{\circ}, \mathrm{m} \angle K=(x+14)^{\circ}$ , and $\mathrm{m} \angle L=(3 x+12)^{\circ}$ . What is the value of $x$ ? $\newline$ Answer:

View step-by-step help

View step-by-step help

Find trigonometric functions using a calculator

Full solution

Q. In

\triangle \mathrm{JKL}, \mathrm{m} \angle J=(5 x+1)^{\circ}, \mathrm{m} \angle K=(x+14)^{\circ}

, and

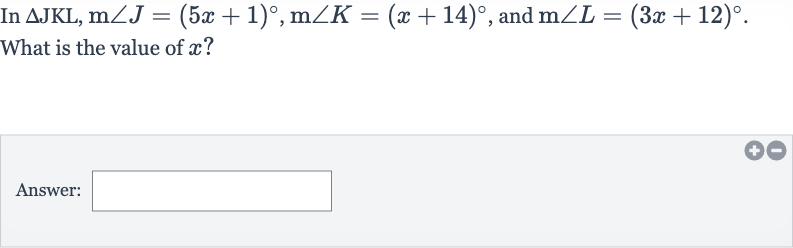
\mathrm{m} \angle L=(3 x+12)^{\circ}

. What is the value of

x

?

\newline

Answer:

Write Equation: Since triangle JKL is a triangle, the sum of its angles must be $180$ degrees. So, we can write the equation: $\newline$ $(5x + 1) + (x + 14) + (3x + 12) = 180$
Add Terms: Now, let's add up all the $x$ terms and the constant terms: $5x + x + 3x + 1 + 14 + 12 = 180$
Combine Like Terms: Combining like terms gives us: $9x + 27 = 180$
Isolate $x$ Term: Subtract $27$ from both sides to isolate the term with $x$ : $9x = 180 - 27$
Subtraction: Now, let's do the subtraction: $9x = 153$
Divide to Solve: Finally, divide both sides by $9$ to solve for $x$ : $x = \frac{153}{9}$
Divide to Solve: Finally, divide both sides by $9$ to solve for $x$ : $x = \frac{153}{9}$ And here's the division: $x = 17$

More problems from Find trigonometric functions using a calculator

Question

Find all solutions with

0^\circ \leq \theta \leq 180^\circ

. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.

\newline

\cos(\theta) = -1

\newline

\underline{\hspace{2em}}^\circ

Posted 7 months ago

Question

Kimi's school is

15

kilometers west of her house and

8

kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?

\newline

\_\_\_\_\_

Posted 7 months ago

Question

Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.

\newline

\cos 35^\circ =

Posted 7 months ago

Question

Find all solutions with

-90^\circ \leq \theta \leq 90^\circ

. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.

\newline

\csc(\theta) = -1

\newline

\_\_\_\_\,^\circ

Posted 8 months ago

Question

Evaluate. Write your answer in simplified, rationalized form. Do not round.

\newline

\cot 30^\circ =

Posted 7 months ago

Question

The terminal side of an angle

\theta

in standard position intersects the unit circle at

(\frac{84}{85}, \frac{13}{85})

\cos(\theta)

\newline

Write your answer in simplified, rationalized form.

\newline

Posted 7 months ago

Question

-90^\circ < \theta < 90^\circ

. Find the value of

\theta

\newline

\tan(\theta) = 0

\newline

Write your answer in simplified, rationalized form. Do not round.

\newline

\theta =

^\circ

\newline

Posted 8 months ago

Question

Evaluate. Write your answer in simplified, rationalized form. Do not round.

\newline

\csc 60^\circ =

Posted 8 months ago

Question

\theta

is an acute angle. Find the value of

\theta

\newline

\sec(\theta) = \sqrt{2}

\newline

\theta =

\degree

Posted 7 months ago

Question

Evaluate. Write your answer in simplified, rationalized form. Do not round.

\newline

\cos 90^\circ =

Posted 9 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant