Resources

Resources

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

$In /_\JKL,j=4.1cm,l=1.2cm and /_L=29^(@). Find all possible values of /_J, to the nearest 1oth of a degree. Answer:$

In $\triangle \mathrm{JKL}, j=4.1 \mathrm{~cm}, l=1.2 \mathrm{~cm}$ and $\angle \mathrm{L}=29^{\circ}$ . Find all possible values of $\angle \mathrm{J}$ , to the nearest $10$ th of a degree. $\newline$ Answer:

Full solution

Q. In

\triangle \mathrm{JKL}, j=4.1 \mathrm{~cm}, l=1.2 \mathrm{~cm}

and

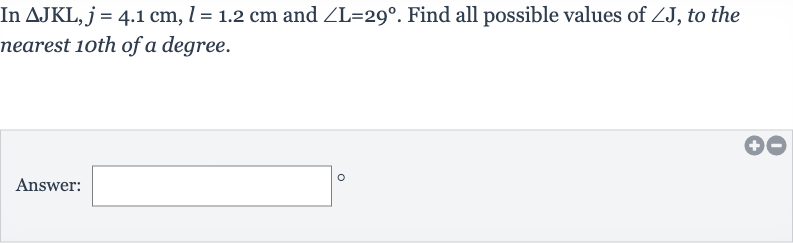
\angle \mathrm{L}=29^{\circ}

. Find all possible values of

\angle \mathrm{J}

, to the nearest

10

th of a degree.

\newline

Answer:

Apply Law of Sines: To find the possible values of $\angle J$ , we can use the Law of Sines, which relates the lengths of sides of a triangle to the sines of its opposite angles. The Law of Sines states that for any triangle $ABC$ with sides $a$ , $b$ , and $c$ opposite angles $A$ , $B$ , and $C$ respectively, the following ratio holds true: $(\sin A)/a = (\sin B)/b = (\sin C)/c$ . We will apply this to triangle $JKL$ .
Find length of side $k$ : First, we need to find the length of side $k$ opposite angle $/_L$ . We can use the Law of Sines to find this. We have two sides and one angle, so we can write the equation as $\frac{\sin L}{l} = \frac{\sin J}{j}$ . We know $L$ and $l$ , so we can solve for $\sin J$ . $\frac{\sin 29^\circ}{1.2} = \frac{\sin J}{4.1}$
Calculate $\sin 29^\circ$ : Now we calculate $\sin 29^\circ$ using a calculator. $\sin 29^\circ \approx 0.4848$
Substitute $\sin 29^\circ$ : Substitute the value of $\sin 29^\circ$ into the equation and solve for $\sin J$ . $\frac{0.4848}{1.2} = \frac{\sin J}{4.1}$ $\sin J \approx \frac{0.4848 \times 4.1}{1.2}$
Perform multiplication and division: Perform the multiplication and division to find $\sin J$ . $\sin J \approx \frac{1.98728}{1.2}$ $\sin J \approx 1.6561$