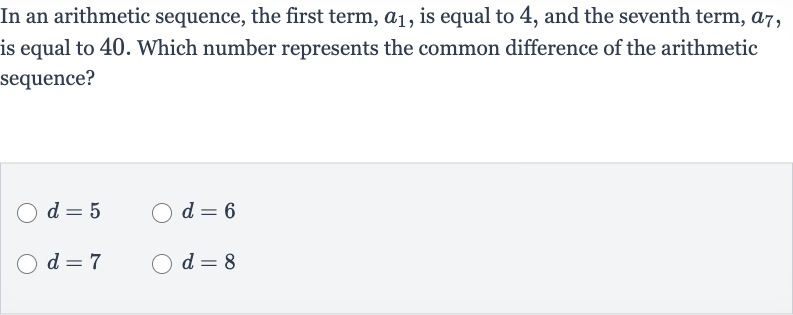Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

In an arithmetic sequence, the first term,
a_(1), is equal to 4 , and the seventh term,
a_(7), is equal to 40 . Which number represents the common difference of the arithmetic sequence?

d=5

d=6

d=7

d=8

In an arithmetic sequence, the first term, $a_{1}$ , is equal to $4$ , and the seventh term, $a_{7}$ , is equal to $40$ . Which number represents the common difference of the arithmetic sequence? $\newline$ $d=5$ $\newline$ $d=6$ $\newline$ $d=7$ $\newline$ $d=8$

View step-by-step help

View step-by-step help

Convert a recursive formula to an explicit formula

Full solution

Q. In an arithmetic sequence, the first term,

a_{1}

, is equal to

4

, and the seventh term,

a_{7}

, is equal to

40

. Which number represents the common difference of the arithmetic sequence?

\newline

d=5

\newline

d=6

\newline

d=7

\newline

d=8

Identify Given Terms: Identify the given terms in the sequence. $\newline$ We are given the first term $a_{1}$ and the seventh term $a_{7}$ of an arithmetic sequence. $\newline$ $a_{1} = 4$ $\newline$ $a_{7} = 40$
Use Formula for nth Term: Use the formula for the nth term of an arithmetic sequence to express $a_{7}$ . The nth term of an arithmetic sequence is given by $a_{n} = a_{1} + (n - 1)d$ , where $d$ is the common difference. For the seventh term, $n = 7$ , so we have: $a_{7} = a_{1} + (7 - 1)d$
Substitute and Solve: Substitute the known values into the formula and solve for $d$ . $a_{7} = 40$ $a_{1} = 4$ $40 = 4 + (7 - 1)d$ $40 = 4 + 6d$
Isolate and Solve: Isolate $d$ and solve the equation. $40 = 4 + 6d$ $40 - 4 = 6d$ $36 = 6d$ $d = \frac{36}{6}$ $d = 6$

More problems from Convert a recursive formula to an explicit formula

Question

Find the sum of the finite arithmetic series.

\sum_{n=1}^{10} (7n+4)

\newline

Posted 3 months ago

Question

Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`

Posted 2 months ago

Question

Type the missing number in this sequence: `2, 4 8`, ______,`32`

Posted 2 months ago

Question

What kind of sequence is this?

2, 10, 50, 250, \ldots

Choices:Choices:

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 2 months ago

Question

What is the missing number in this pattern?

1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_

Posted 2 months ago

Question

Classify the series.

\sum_{n = 0}^{12} (n + 2)^3

\newline

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 2 months ago

Question

Find the first three partial sums of the series.

\newline

1 + 6 + 11 + 16 + 21 + 26 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 2 months ago

Question

Find the third partial sum of the series.

\newline

3 + 9 + 15 + 21 + 27 + 33 + \cdots

\newline

Write your answer as an integer or a fraction in simplest form.

\newline

S_3 =

Posted 2 months ago

Question

Find the first three partial sums of the series.

\newline

1 + 7 + 13 + 19 + 25 + 31 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 3 months ago

Question

Does the infinite geometric series converge or diverge?

\newline

1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots

\newline

\newline

\text{[A]converge}

\newline

\text{[B]diverge}

Posted 2 months ago