AI tutor
Full solution
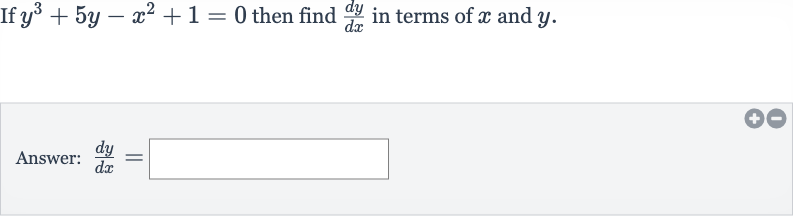
Q. If then find in terms of and .Answer:
- Implicit Differentiation: Differentiate both sides of the equation with respect to . We will use implicit differentiation because is a function of . Differentiate with respect to : Differentiate with respect to : Differentiate with respect to : Differentiate with respect to :
- Write Differentiated Equation: Write down the differentiated equation.
- Solve for (\frac{dy}{dx}): Solve for \((\frac{dy}{dx}).\(\newlineFactor out (\frac{dy}{dx}) from the terms that contain it:\(\newline(\frac{dy}{dx})(\(3y^ + ) = xNow, divide both sides by (\(3y^ + ) to isolate (\frac{dy}{dx}):\(\newline\((\frac{dy}{dx}) = \frac{\(2\)x}{\(3\)y^\(2\) + \(5\)}
More problems from Transformations of quadratic functions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help