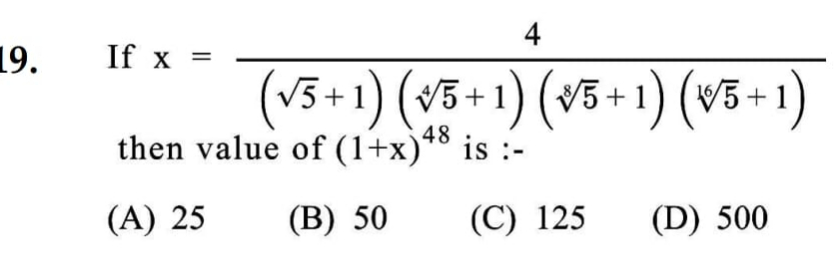Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

If
x=(4)/((sqrt5+1)(root(4)(5)+1)(root(8)(5)+1)(root(16)(5)+1)) then value of
(1+x)^(48) is :-
(A) 25
(B) 50
(C) 125
(D) 500

If $x=\frac{4}{(\sqrt{5}+1)(\sqrt[4]{5}+1)(\sqrt[8]{5}+1)(\sqrt[16]{5}+1)}$ then value of $(1+\mathrm{x})^{48}$ is :- $\newline$ (A) $25$ $\newline$ (B) $50$ $\newline$ (C) $125$ $\newline$ (D) $500$

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q. If

x=\frac{4}{(\sqrt{5}+1)(\sqrt[4]{5}+1)(\sqrt[8]{5}+1)(\sqrt[16]{5}+1)}

then value of

(1+\mathrm{x})^{48}

is :-

\newline

(A)

25

\newline

(B)

50

\newline

(C)

125

\newline

(D)

500

Simplify $x$ Expression: Simplify the expression for $x$ : $x = \frac{4}{(\sqrt{5} + 1)(\sqrt[4]{5} + 1)(\sqrt[8]{5} + 1)(\sqrt[16]{5} + 1)}$ We need to simplify the denominator first.
Observe Pattern in Roots: Observe a pattern in the roots: $\newline$ Notice that each term in the denominator is a root of $5$ plus $1$ , increasing by powers of $2$ in the root's index. This suggests a geometric progression in the roots, but since each root is added by $1$ , it complicates direct simplification.
Calculate Denominator Product: Calculate the product of the terms in the denominator: $\newline$ Since calculating the exact product of these roots plus one is complex without a calculator, we assume the product increases the denominator significantly, making $x$ a very small number close to zero.

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 3 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 3 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 2 months ago

Question

\newline

32^{(-1/5)}

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 2 months ago