Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

If
f(x)=3^(x^(2)-9)+11, what is the value of
f(-3), to the nearest thousandth (if necessary)?
Answer:

If $f(x)=3^{x^{2}-9}+11$ , what is the value of $f(-3)$ , to the nearest thousandth (if necessary)? $\newline$ Answer:

View step-by-step help

View step-by-step help

Find trigonometric functions using a calculator

Full solution

Q. If

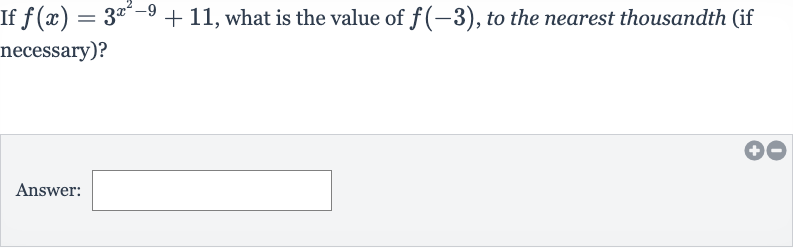
f(x)=3^{x^{2}-9}+11

, what is the value of

f(-3)

, to the nearest thousandth (if necessary)?

\newline

Answer:

Substitute $x$ with $-3$ : To find the value of $f(-3)$ , we need to substitute $x$ with $-3$ in the function $f(x) = 3^{(x^2-9)}+11$ .
Calculate exponent for $x = -3$ : First, calculate the exponent part of the function for $x = -3$ : $(-3)^2 - 9$ . $\newline$ $(-3)^2 = 9$ , so we have $9 - 9 = 0$ .
Raise $3$ to power of $0$ : Now, we raise $3$ to the power of $0$ , which is $3^0$ . Since any number raised to the power of $0$ is $1$ , we have $3^0 = 1$ .
Add $11$ to result: Next, we add $11$ to the result of $3^0$ , which is $1$ . So, $1 + 11 = 12$ .
Find value of $f(-3)$ : The value of $f(-3)$ is therefore $12$ . Since $12$ is an integer, there is no need to round it to the nearest thousandth.

More problems from Find trigonometric functions using a calculator

Question

Find all solutions with

0^\circ \leq \theta \leq 180^\circ

. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.

\newline

\cos(\theta) = -1

\newline

\underline{\hspace{2em}}^\circ

Posted 7 months ago

Question

Kimi's school is

15

kilometers west of her house and

8

kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?

\newline

\_\_\_\_\_

Posted 7 months ago

Question

Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.

\newline

\cos 35^\circ =

Posted 7 months ago

Question

Find all solutions with

-90^\circ \leq \theta \leq 90^\circ

. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.

\newline

\csc(\theta) = -1

\newline

\_\_\_\_\,^\circ

Posted 8 months ago

Question

Evaluate. Write your answer in simplified, rationalized form. Do not round.

\newline

\cot 30^\circ =

Posted 7 months ago

Question

The terminal side of an angle

\theta

in standard position intersects the unit circle at

(\frac{84}{85}, \frac{13}{85})

\cos(\theta)

\newline

Write your answer in simplified, rationalized form.

\newline

Posted 7 months ago

Question

-90^\circ < \theta < 90^\circ

. Find the value of

\theta

\newline

\tan(\theta) = 0

\newline

Write your answer in simplified, rationalized form. Do not round.

\newline

\theta =

^\circ

\newline

Posted 8 months ago

Question

Evaluate. Write your answer in simplified, rationalized form. Do not round.

\newline

\csc 60^\circ =

Posted 8 months ago

Question

\theta

is an acute angle. Find the value of

\theta

\newline

\sec(\theta) = \sqrt{2}

\newline

\theta =

\degree

Posted 7 months ago

Question

Evaluate. Write your answer in simplified, rationalized form. Do not round.

\newline

\cos 90^\circ =

Posted 9 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant