Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

If f(1)=7 and f(n)=4f(n-1)+n then find the value of f(3). Answer:

If f(1)=7 f(1)=7 and f(n)=4f(n−1)+n f(n)=4 f(n-1)+n then find the value of f(3) f(3) .\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Evaluate functionsright chevron icon

Full solution

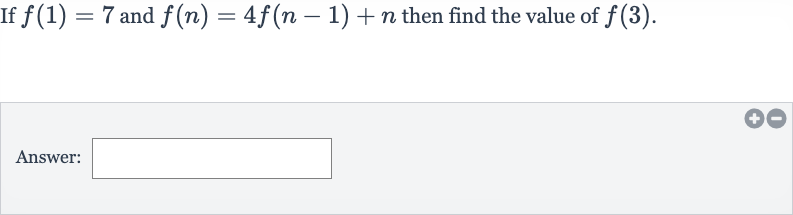
Q. If f(1)=7 f(1)=7 and f(n)=4f(n−1)+n f(n)=4 f(n-1)+n then find the value of f(3) f(3) .\newlineAnswer:
  1. Given f(1)=7f(1) = 7: We are given that f(1)=7f(1) = 7. To find f(3)f(3), we first need to find f(2)f(2) using the recursive formula f(n)=4f(n−1)+nf(n) = 4f(n-1) + n.\newlineSubstitute n=2n = 2 into the formula to find f(2)f(2).\newlinef(2)=4f(2−1)+2f(2) = 4f(2-1) + 2\newlinef(2)=4f(1)+2f(2) = 4f(1) + 2\newlinef(2)=4(7)+2f(2) = 4(7) + 2\newlinef(1)=7f(1) = 700\newlinef(1)=7f(1) = 711
  2. Find f(2)f(2): Now that we have f(2)=30f(2) = 30, we can use it to find f(3)f(3) using the same recursive formula.\newlineSubstitute n=3n = 3 into the formula to find f(3)f(3).\newlinef(3)=4f(3−1)+3f(3) = 4f(3-1) + 3\newlinef(3)=4f(2)+3f(3) = 4f(2) + 3\newlinef(3)=4(30)+3f(3) = 4(30) + 3\newlinef(3)=120+3f(3) = 120 + 3\newlinef(3)=123f(3) = 123

More problems from Evaluate functions

Question
What is the domain of this function?\newline(9,–2)(6,–10)(–3,9)(5,2)(9,–2)(6,–10)(–3,9)(5,2)\newlineChoices:\newline(A){–3,5,6,9}(B){–10,–2,2,9}(C){2,5,6,9}(D){–6,–3,5,9}(A)\{–3,5,6,9\}\newline(B)\{–10,–2,2,9\}\newline(C)\{2,5,6,9\}\newline(D)\{–6,–3,5,9\}
Get tutor helpright-arrow

Posted 8 months ago

Question
Look at this set of ordered pairs:\newline(2,14)(2, 14)\newline(10,12)(10, 12)\newline(3,−19)(3, -19)\newlineIs this relation a function?\newlineChoices:\newline[[yes]\text{[[yes]}[no]]\text{[no]]}
Get tutor helpright-arrow

Posted 8 months ago

Question
Use the following function rule to find f(11) f(11) .\newlinef(x)=−10−7x f(x) = -10 - 7x \newlinef(11)= f(11) = _____
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the slope of the line y=−3x−25 y = -3x - \frac{2}{5} .\newlineSimplify your answer and write it as a proper fraction, improper fraction, or integer.\newline_____\_\_\_\_\_
Get tutor helpright-arrow

Posted 8 months ago

Question
A line has a slope of 33 and passes through the point (−2,−10)(-2,-10). Write its equation in slope-intercept form.\newlineWrite your answer using integers, proper fractions, and improper fractions in simplest form.
Get tutor helpright-arrow

Posted 8 months ago

Question
What is the range of this function?\newliney = |x|\newlineChoices:\newlineall real numbers\text{all real numbers}\newline{y∣y≥0}\{y \mid y \geq 0\}\newline{y∣y≤0}\{y \mid y \leq 0\}\newline{y∣y>0}\{y \mid y > 0\}
Get tutor helpright-arrow

Posted 9 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 1 1 unit down of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
What is the domain of this function?\newline(8,–1)(7,–11)(–4,10)(4,3)(8,–1)(7,–11)(–4,10)(4,3)\newlineChoices: \newline(A){–4,4,7,8}(A)\{–4,4,7,8\}\newline(B){–11,–1,3,10}(B)\{–11,–1,3,10\}\newline(C){3,4,7,8}(C)\{3,4,7,8\}\newline(D){–7,–4,4,8}(D)\{–7,–4,4,8\}
Get tutor helpright-arrow

Posted 10 months ago

Question
What is the domain of this function?\newline(10, –3)(2, –9)(–5, 8)(3, 1)(10,\,–3)(2,\,–9)(–5,\,8)(3,\,1)\newlineChoices:\newline[{–5,2,3,10}][{–9, –3,1,8}][{1,2,3,10}][{–10, –5,2,3}][\{–5,2,3,10\}][\{–9,\,–3,1,8\}][\{1,2,3,10\}][\{–10,\,–5,2,3\}]
Get tutor helpright-arrow

Posted 8 months ago

Question
What is the domain of this function?\newline(1,–4)(9,–12)(–6,11)(7,5)(1,–4)(9,–12)(–6,11)(7,5)\newlineChoices:(A){–6,1,7,9}\newline\\(A)\{–6,1,7,9\}\newline(B){–12,–4,5,11}(B)\{–12,–4,5,11\}\newline(C{5,1,7,9}(C\{5,1,7,9\}\newline(D){–9,–6,1,7}(D)\{–9,–6,1,7\}
Get tutor helpright-arrow

Posted 8 months ago

View all (97)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant