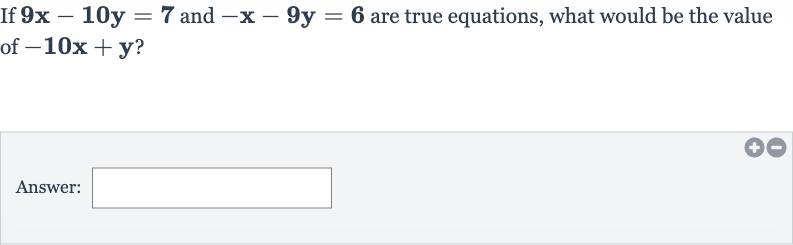If $\mathbf{9 x}-\mathbf{1 0 y}=\mathbf{7}$ and $-\mathbf{x}-\mathbf{9 y}=\mathbf{6}$ are true equations, what would be the value of $-\mathbf{1 0 x}+\mathbf{y}$ ? $\newline$ Answer:

View step-by-step help

Home

Math Problems

Algebra 2

Find trigonometric ratios using multiple identities

Full solution

Q. If

\mathbf{9 x}-\mathbf{1 0 y}=\mathbf{7}

and

-\mathbf{x}-\mathbf{9 y}=\mathbf{6}

are true equations, what would be the value of

-\mathbf{1 0 x}+\mathbf{y}

\newline

Answer:

Equations to Solve: We have two equations: $\newline$ $1$ ) $9x - 10y = 7$ $\newline$ $2$ ) $-x - 9y = 6$ $\newline$ We need to find the value of $-10x + y$ . To do this, we can solve the system of equations for $x$ and $y$ and then substitute these values into the expression $-10x + y$ .
Isolate $x$ : First, let's solve for $x$ using the second equation. We can do this by isolating $x$ on one side of the equation. $\newline$ $-x - 9y = 6$ $\newline$ Multiply both sides by $-1$ to get $x$ by itself: $\newline$ $x = 9y - 6$
Substitute $x$ into $1$ st equation: Now that we have $x$ in terms of $y$ , we can substitute this expression for $x$ into the first equation to solve for $y$ .
Substitute $x = 9y - 6$ into the first equation:
$9(9y - 6) - 10y = 7$
Solve for y: Next, we expand the equation and simplify it to solve for y. $\newline$ $81y - 54 - 10y = 7$ $\newline$ Combine like terms: $\newline$ $71y - 54 = 7$ $\newline$ Add $54$ to both sides: $\newline$ $71y = 61$ $\newline$ Divide both sides by $71$ : $\newline$ $y = \frac{61}{71}$
Substitute $y$ into $x$ expression: Now that we have the value of $y$ , we can substitute it back into the expression for $x$ to find the value of $x$ .
$x = 9y - 6$
$x = 9(\frac{61}{71}) - 6$
Calculate x value: We calculate the value of x by multiplying $9$ by $61/71$ and then subtracting $6$ .
$x = 549 / 71 - 6$
To subtract $6$ , we need to express it as a fraction with the same denominator as $549/71$ :
$x = 549 / 71 - 426 / 71$
$x = (549 - 426) / 71$
$x = 123 / 71$
Substitute $x$ and $y$ into expression: Finally, we substitute the values of $x$ and $y$ into the expression $-10x + y$ to find the value we're looking for. $\newline$ $-10x + y = -10(123 / 71) + (61 / 71)$
Substitute $x$ and $y$ into expression: Finally, we substitute the values of $x$ and $y$ into the expression $-10x + y$ to find the value we're looking for. $\newline$ $-10x + y = -10(123 / 71) + (61 / 71)$ We calculate the value of $-10x + y$ by multiplying $-10$ by $123/71$ and then adding $61/71$ . $\newline$ $y$ $0$ $\newline$ Combine the fractions: $\newline$ $y$ $1$ $\newline$ $y$ $2$