Full solution
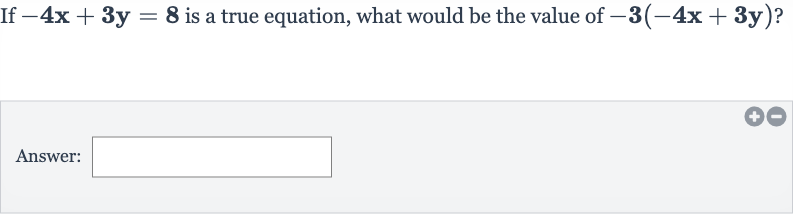
Q. If is a true equation, what would be the value of ?Answer:
- Multiply by : We are given the equation . We need to multiply this entire equation by .Calculation:
- Multiply terms by : Now we will multiply each term inside the parentheses by .Calculation: and So,
- Apply equation property: Since is a true equation, when we multiply both sides by , the right side of the equation also gets multiplied by .Calculation:
- Calculate final result: Now we will multiply by .Calculation: So,