AI tutor
Full solution
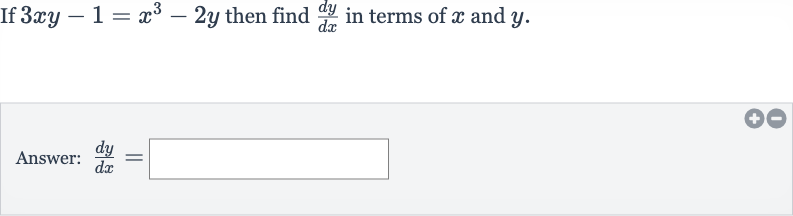
Q. If then find in terms of and .Answer:
- Apply Product Rule: We need to differentiate both sides of the equation with respect to to find . Differentiate the left side using the product rule: , where and . Differentiate the right side with respect to normally.
- Differentiate Left Side: Differentiate the left side: . Using the product rule: . Since , we have . So, .
- Differentiate Right Side: Differentiate the right side: . The derivative of with respect to is . The derivative of with respect to is . So, .
- Equate Derivatives: Now we equate the derivatives from both sides:.Simplify the equation:.
- Group Terms: Group all the terms containing on one side and the rest on the other side:Factor out :
- Solve for : Solve for :.This is the derivative of with respect to in terms of and .
More problems from Transformations of quadratic functions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help