AI tutor
Full solution
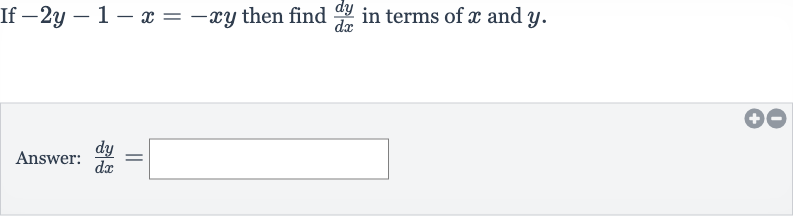
Q. If then find in terms of and .Answer:
- Differentiate left side with respect to : We are given the equation . To find , we need to differentiate both sides of the equation with respect to , treating as a function of (implicit differentiation).
- Differentiate right side with respect to : Differentiate the left side of the equation with respect to . The derivative of with respect to is because is a function of . The derivative of with respect to is , and the derivative of with respect to is .
- Combine differentiated equations: Differentiate the right side of the equation with respect to . The derivative of with respect to is because we use the product rule for differentiation ( of , where and ).
- Isolate terms with (\frac{dy}{dx}): Now we have the differentiated equation: \(\(-2(\frac{dy}{dx}) - = -y - x(\frac{dy}{dx}).
- Add and : We need to solve for . To do this, we'll collect all the terms involving on one side of the equation and the constant terms on the other side.
- Combine like terms: Add to both sides and add to both sides to isolate terms with on one side: .
- Divide both sides to solve: Combine like terms: .
- Divide both sides to solve: Combine like terms: .Now, divide both sides by to solve for : .