AI tutor
Full solution
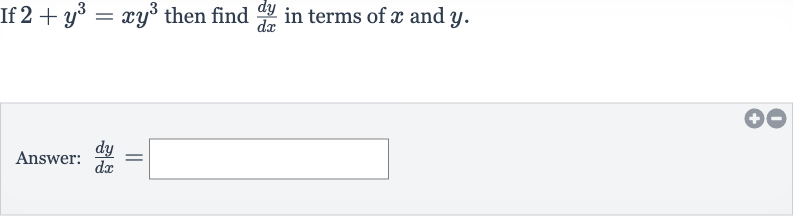
Q. If then find in terms of and .Answer:
- Write Given Equation: Write down the given equation.We have the equation .
- Differentiate with Respect: Differentiate both sides of the equation with respect to . The left side becomes the derivative of with respect to , which is , plus the derivative of with respect to , which is using the chain rule. The right side becomes the derivative of with respect to , which is plus times the derivative of with respect to , which is , using the product rule. So, we have .
- Simplify and Solve: Simplify the equation and solve for . Subtract from both sides to get . This simplifies to .
- Factor Out Common Factor: Factor out . We have . Since is a common factor, we can divide both sides by , assuming is not zero (since would make the original equation , which is not true). This gives us .
- Isolate and Solve: Solve for .Divide both sides by to isolate , which gives us .Since divided by anything is , we have .
More problems from Find trigonometric ratios using reference angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help