Full solution
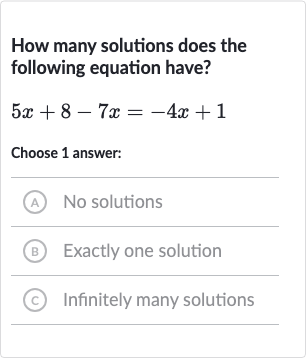
Q. How many solutions does the following equation have?Choose answer:(A) No solutions(B) Exactly one solution(C) Infinitely many solutions
- Combine like terms: Combine like terms on the left side of the equation.This simplifies to:
- Add terms together: Add to both sides to get all the terms on one side.This simplifies to:
- Isolate x term: Subtract from both sides to isolate the term with .This simplifies to:
- Solve for x: Divide both sides by to solve for x.This simplifies to:
- Final solution: Since we have found a value for , the equation has exactly one solution.
More problems from Solve trigonometric equations
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help