Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

h(t)=-16.1t^(2)+100 t
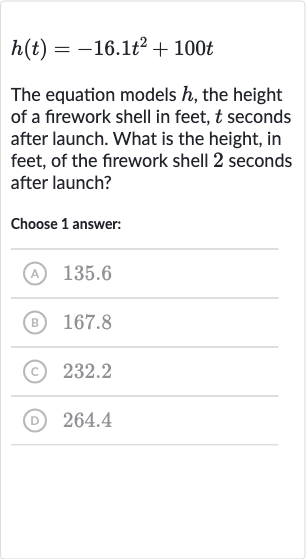
The equation models
h, the height of a firework shell in feet,
t seconds after launch. What is the height, in feet, of the firework shell 2 seconds after launch?
Choose 1 answer:
(A) 135.6
(B) 167.8
(C) 232.2
(D) 264.4

$h(t)=-16.1 t^{2}+100 t$ $\newline$ The equation models $h$ , the height of a firework shell in feet, $t$ seconds after launch. What is the height, in feet, of the firework shell $2$ seconds after launch? $\newline$ Choose $1$ answer: $\newline$ (A) $135$ . $6$ $\newline$ (B) $167$ . $8$ $\newline$ (C) $232$ . $2$ $\newline$ (D) $264$ . $4$

View step-by-step help

View step-by-step help

Solve a system of equations using any method: word problems

Full solution

Q.

h(t)=-16.1 t^{2}+100 t

\newline

The equation models

h

, the height of a firework shell in feet,

t

seconds after launch. What is the height, in feet, of the firework shell

2

seconds after launch?

\newline

Choose

1

answer:

\newline

(A)

135

.

6

\newline

(B)

167

.

8

\newline

(C)

232

.

2

\newline

(D)

264

.

4

Identify Given Equation: Identify the given equation and the time at which we need to find the height. $\newline$ The given equation is $h(t) = -16.1t^2 + 100t$ , which models the height of a firework shell in feet, $t$ seconds after launch. We need to find the height at $t = 2$ seconds.
Substitute Value of $t$ : Substitute the value of $t$ into the equation to find the height at that time. $\newline$ Using $t = 2$ seconds, we substitute it into the equation to get $h(2) = -16.1(2)^2 + 100(2)$ .
Calculate $h(2)$ : Calculate the value of $h(2)$ by performing the operations. $\newline$ First, calculate the square of $2$ , which is $2^2 = 4$ . $\newline$ Then multiply this by $-16.1$ to get $-16.1 \times 4 = -64.4$ . $\newline$ Next, multiply $100$ by $2$ to get $100 \times 2 = 200$ . $\newline$ Now, add these two results together to find the height: $h(2) = -64.4 + 200$ .
Perform Addition: Perform the addition to find the final height. $h(2) = -64.4 + 200 = 135.6$ feet.

More problems from Solve a system of equations using any method: word problems

Question

Solve using elimination.

\newline

x + 6y = -15

\newline

-2x + 6y = 12

\newline

(\_,\_)

Posted 5 months ago

Question

(1,1)

a solution to this system of equations?

\newline

8x + y = 9

\newline

6x + 12y = 18

\newline

\newline

\newline

Posted 5 months ago

Question

How many solutions does the system of equations below have?

\newline

7

\newline

7

\newline

\newline

\text{[A]no solution}

\newline

\text{[B]one solution}

\newline

\text{[C]infinitely many solutions}

Posted 7 months ago

Question

Which describes the system of equations below?

\newline

y = \frac{1}{7}x - 10

\newline

y = \frac{1}{7}x - 10

\newline

\newline

\text{[A]consistent and independent}

\newline

\text{[B]consistent and dependent}

\newline

\text{[C]inconsistent}

Posted 5 months ago

Question

Solve using substitution.

\newline

y = -5

\newline

-4x + 3y = 17

\newline

Posted 5 months ago

Question

Write a system of equations to describe the situation below, solve using substitution, and fill in the blanks.

\newline

Last Wednesday, two friends met up after school to read the book they were both assigned in Literature class. Bryan can read

2

pages per minute, and he had already read

98

pages. Jayla, who has a reading speed of

3

pages per minute, had read

48

pages. Eventually they had read the same number of pages. How long did that take? How many pages had each of them read?

\newline

\_\_\_\_

minutes, Bryan and Jayla had each read

\_\_\_\_

Posted 5 months ago

Question

Write a system of equations to describe the situation below, solve using elimination, and fill in the blanks.

\newline

At the Castroville Ice Cream Parlor, one group of friends ordered

1

small serving of ice cream and

3

large servings of ice cream for

20

. Another group of friends ordered

1

small serving of ice cream and

4

large servings of ice cream for

26

. How much does the ice cream cost?

\newline

The ice cream costs `\$`_____ for a small serving and `\$`_____ for a large serving.

Posted 5 months ago

Question

\newline

y = -1

\newline

-2x - 4y = 8

\newline

(_____ , _____)

Posted 7 months ago

Question

Write a system of equations to describe the situation below, solve using any method, and fill in the blanks.

\newline

There are two mystery numbers. The sum of

3

times the first number and

3

times the second number is

-18

2

times the first number and

3

times the second number is

-13

. What are the two numbers?

\newline

The first number is ______ , and the second number is ______.

Posted 7 months ago

Question

A teacher purchased

300

colored pencils for an upcoming project. The pencils she ordered come in packs of

20

30

14

packs in all. Write a system of equations to find the number of

20

(x)

30

(y)

the art teacher ordered.

Posted 8 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant