Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

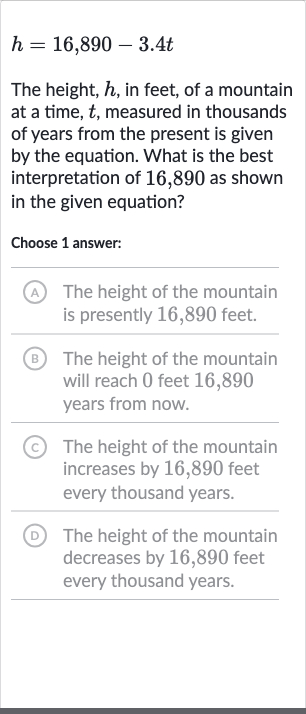
h=16,890-3.4 t The height, h, in feet, of a mountain at a time, t, measured in thousands of years from the present is given by the equation. What is the best interpretation of 16,890 as shown in the given equation? Choose 1 answer: A The height of the mountain is presently 16,890 feet. (B) The height of the mountain will reach 0 feet 16,890 years from now. (c) The height of the mountain increases by 16,890 feet every thousand years. (D) The height of the mountain decreases by 16,890 feet every thousand years.

h=16,890−3.4t h=16,890-3.4 t \newlineThe height, h h , in feet, of a mountain at a time, t t , measured in thousands of years from the present is given by the equation. What is the best interpretation of 1616,890890 as shown in the given equation?\newlineChoose 11 answer:\newline(A) The height of the mountain is presently 1616,890890 feet.\newline(B) The height of the mountain will reach 00 feet 1616,890890 years from now.\newline(C) The height of the mountain increases by 1616,890890 feet every thousand years.\newline(D) The height of the mountain decreases by 1616,890890 feet every thousand years.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Interpret parts of quadratic expressions: word problemsright chevron icon

Full solution

Q. h=16,890−3.4t h=16,890-3.4 t \newlineThe height, h h , in feet, of a mountain at a time, t t , measured in thousands of years from the present is given by the equation. What is the best interpretation of 1616,890890 as shown in the given equation?\newlineChoose 11 answer:\newline(A) The height of the mountain is presently 1616,890890 feet.\newline(B) The height of the mountain will reach 00 feet 1616,890890 years from now.\newline(C) The height of the mountain increases by 1616,890890 feet every thousand years.\newline(D) The height of the mountain decreases by 1616,890890 feet every thousand years.
  1. Equation Analysis: Analyze the equation h=16,890−3.4th=16,890-3.4t to understand what each term represents.\newlineThe equation is a linear equation where hh represents the height of the mountain at time tt, and tt is measured in thousands of years from the present.
  2. Constant Term: Consider the term 16,89016,890 in the equation.\newlineThis term is a constant and does not depend on the variable tt. It represents the initial state of the height of the mountain when t=0t=0, which is the present time.
  3. Evaluation at t=0t=0: Evaluate the equation at t=0t=0 to confirm the interpretation of 16,89016,890. If we substitute t=0t=0 into the equation, we get h=16,890−3.4(0)h=16,890-3.4(0), which simplifies to h=16,890h=16,890.
  4. Interpretation of 16,89016,890: Determine the best interpretation of 16,89016,890 based on the previous steps.\newlineSince 16,89016,890 is the height of the mountain at the present time (t=0)(t=0), the best interpretation is that the height of the mountain is presently 16,89016,890 feet.

More problems from Interpret parts of quadratic expressions: word problems

Question
Solve by completing the square.\newlinem2−10m−29=0m^2 - 10m - 29 = 0\newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newline`m` = ____ or `m` = _____
Get tutor helpright-arrow

Posted 8 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 5 5 units up of f(x)=x2 f(x)=x^2 .\newlineWrite your answer in the form a(x–h)2+k a(x–h)^2+k , where a a , h h , and k k are integers.\newlineg(x)= g(x)= ____
Get tutor helpright-arrow

Posted 7 months ago

Question
What is the range of this quadratic function?\newliney=x2−4x+4y = x^2 - 4x + 4\newlineChoices:\newline{y∣y≥2}\left\{y \mid y \geq 2\right\}\newline{y∣y≤0}\left\{y \mid y \leq 0\right\}\newline{y∣y≥0}\left\{y \mid y \geq 0\right\}\newlineall real numbers\text{all real numbers}
Get tutor helpright-arrow

Posted 5 months ago

Question
Write the equation of the parabola that passes through the points (1,0)(1,0), (2,0)(2,0), and (3,–16)(3,\text{–}16). Write your answer in the form y=a(x–p)(x–q)y = a(x – p)(x – q), where aa, pp, and qq are integers, decimals, or simplified fractions.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.\newlinef2+8f+_____f^2 + 8f + \_\_\_\_\_
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve for h h .\newlineh2+39h=0 h^2 + 39h = 0 \newline\newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.\newlineh= h = ____\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Write a quadratic function with zeros −9-9 and −7-7.\newlineWrite your answer using the variable xx and in standard form with a leading coefficient of 11.\newlinef(x)=_____f(x) = \_\_\_\_\_
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the equation of the axis of symmetry for the parabola y=x2y = x^2. \newlineSimplify any numbers and write them as proper fractions, improper fractions, or integers.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 4 months ago

Question
Find g(x)g(x), where g(x)g(x) is the translation 88 units up of f(x)=x2f(x) = x^2.\newlineWrite your answer in the form a(x–h)2+ka(x – h)^2 + k, where aa, hh, and kk are integers.\newlineg(x)=g(x) = ______\newline
Get tutor helpright-arrow

Posted 4 months ago

Question
Solve for xx.\newlinex2=1x^2 = 1\newline\newlineWrite your answer in simplified, rationalized form.\newlinex=x = ______ or x=x = ______\newline
Get tutor helpright-arrow

Posted 5 months ago

View all (145)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant